Regression Test for Funnel Plot Asymmetry

Function to carry out (various versions of) Egger's regression test for funnel plot asymmetry.

regtest(x, vi, sei, ni, subset, data,
        model="rma", predictor="sei", ret.fit=FALSE, digits, ...)

Arguments

x: a vector with the observed effect sizes or outcomes or an object of class "rma".
vi: vector with the corresponding sampling variances (ignored if x is an object of class "rma").
sei: vector with the corresponding standard errors (note: only one of the two, vi or sei, needs to be specified).
ni: optional vector with the corresponding sample sizes (only relevant when using the sample sizes (or a transformation thereof) as predictor).
subset: optional (logical or numeric) vector to specify the subset of studies that should be included in the test (ignored if x is an object of class "rma").
data: optional data frame containing the variables given to the arguments above.
model: either "rma" or "lm" to specify the type of model to use for the regression test. See ‘Details’.
predictor: either "sei" "vi", "ni", "ninv", "sqrtni", or "sqrtninv" to specify the predictor to use for the regression test. See ‘Details’.
ret.fit: logical to specify whether the full results from the fitted model should also be returned.
digits: optional integer to specify the number of decimal places to which the printed results should be rounded.
...: other arguments.

Details

Various tests for funnel plot asymmetry have been suggested in the literature, including the rank correlation test by Begg and Mazumdar (1994) and the regression test by Egger et al. (1997). Extensions, modifications, and further developments of the regression test are described (among others) by Macaskill, Walter, and Irwig (2001), Sterne and Egger (2005), Harbord, Egger, and Sterne (2006), Peters et al. (2006), Rücker et al. (2008), and Moreno et al. (2009). The various versions of the regression test differ in terms of the model (either a weighted regression model with a multiplicative dispersion term or a fixed/mixed-effects meta-regression model is used), in terms of the predictor variable that the observed effect sizes or outcomes are hypothesized to be related to when publication bias is present (suggested predictors include the standard error, the sampling variance, and the sample size or transformations thereof), and in terms of the outcome measure used (e.g., for \(2 \times 2\) table data, one has the choice between various outcome measures). The idea behind the various tests is the same though: If there is a relationship between the observed effect sizes or outcomes and the chosen predictor, then this usually implies asymmetry in the funnel plot, which in turn may be an indication of publication bias.

The regtest function can be used to carry out various versions of the regression test. One can either pass a vector with the observed effect sizes or outcomes (via x) and the corresponding sampling variances via vi (or the standard errors via sei) to the function or an object of class "rma".

The model type for the regression test is chosen via the model argument, with model="lm" for a weighted regression model with a multiplicative dispersion term or model="rma" for a (mixed-effects) meta-regression model (the default).

The predictor for the test is chosen via the predictor argument:

predictor="sei" for the standard errors (the default),
predictor="vi" for the sampling variances,
predictor="ni" for the sample sizes,
predictor="ninv" for the inverse of the sample sizes,
predictor="sqrtni" for the square root of the sample sizes, or
predictor="sqrtninv" for the inverse square root of the sample sizes.

The outcome measure used for the regression test is simply determined by the values passed to the function or the measure that was used in fitting the original model (when passing an object of class "rma" to the function).

When using the sample sizes (or a transformation thereof) as the predictor, one can use the ni argument to specify the sample sizes. When x is a vector with the observed effect sizes or outcomes and it was computed with escalc, then the sample sizes should automatically be stored as an attribute of x and ni does not need to be specified. This should also be the case when passing an object of class "rma" to the function and the input to the model fitting function came from escalc.

When passing an object of class "rma" to the function, arguments such as method, weighted, and test as used during the initial model fitting are also used for the regression test. If the model already included one or more moderators, then regtest will add the chosen predictor to the moderator(s) already included in the model. This way, one can test for funnel plot asymmetry after accounting first for the influence of the moderator(s) already included in the model.

The model used for conducting the regression test can also be used to obtain a ‘limit estimate’ of the (average) true effect or outcome. In particular, when the standard errors, sampling variances, or inverse (square root) sample sizes are used as the predictor, the model intercept in essence reflects the estimate under infinite precision. This is sometimes (cautiously) interpreted as an estimate of the (average) true effect or outcome that is adjusted for publication bias.

Value

An object of class "regtest". The object is a list containing the following components:

model: the model used for the regression test.
predictor: the predictor used for the regression test.
zval: the value of the test statistic.
pval: the corresponding p-value
dfs: the degrees of freedom of the test statistic (if the test is based on a t-distribution).
fit: the full results from the fitted model.
est: the limit estimate (only for predictors "sei" "vi", "ninv", or "sqrtninv" and when the model does not contain any additional moderators; NULL otherwise).
ci.lb: lower bound of the confidence interval for the limit estimate.
ci.ub: upper bound of the confidence intervals for the limit estimate.

The results are formatted and printed with the print function.

Note

The classical ‘Egger test’ is obtained by setting model="lm" and predictor="sei". For the random/mixed-effects version of the test, set model="rma" (this is the default). See Sterne and Egger (2005) for details on these two types of models/tests.

When conducting a classical ‘Egger test’, the test of the limit estimate is the same as the ‘precision-effect test’ (PET) of Stanley and Doucouliagos (2014). The limit estimate when using the sampling variance as predictor is sometimes called the ‘precision-effect estimate with SE’ (PEESE) (Stanley & Doucouliagos, 2014). A conditional procedure where we use the limit estimate when PET is not significant (i.e., when using the standard error as predictor) and the PEESE (i.e., when using the sampling variance as predictor) when PET is significant is sometimes called the PET-PEESE procedure (Stanley & Doucouliagos, 2014).

All of the tests do not directly test for publication bias, but for a relationship between the observed effect sizes or outcomes and the chosen predictor. If such a relationship is present, then this usually implies asymmetry in the funnel plot, which in turn may be an indication of publication bias. However, it is important to keep in mind that there can be other reasons besides publication bias that could lead to asymmetry in the funnel plot.

Author

Wolfgang Viechtbauer (wvb@metafor-project.org, https://www.metafor-project.org).

References

Begg, C. B., & Mazumdar, M. (1994). Operating characteristics of a rank correlation test for publication bias. Biometrics, 50(4), 1088–1101. https://doi.org/10.2307/2533446

Egger, M., Davey Smith, G., Schneider, M., & Minder, C. (1997). Bias in meta-analysis detected by a simple, graphical test. British Medical Journal, 315(7109), 629–634. https://doi.org/10.1136/bmj.315.7109.629

Harbord, R. M., Egger, M., & Sterne, J. A. C. (2006). A modified test for small-study effects in meta-analyses of controlled trials with binary endpoints. Statistics in Medicine, 25(20), 3443–3457. https://doi.org/10.1002/sim.2380

Macaskill, P., Walter, S. D., & Irwig, L. (2001). A comparison of methods to detect publication bias in meta-analysis. Statistics in Medicine, 20(4), 641–654. https://doi.org/10.1002/sim.698

Moreno, S. G., Sutton, A. J., Ades, A. E., Stanley, T. D., Abrams, K. R., Peters, J. L., & Cooper, N. J. (2009). Assessment of regression-based methods to adjust for publication bias through a comprehensive simulation study. BMC Medical Research Methodology, 9, 2. https://doi.org/10.1186/1471-2288-9-2

Peters, J. L., Sutton, A. J., Jones, D. R., Abrams, K. R., & Rushton, L. (2006). Comparison of two methods to detect publication bias in meta-analysis. Journal of the American Medical Association, 295(6), 676–680. https://doi.org/10.1001/jama.295.6.676

Rücker, G., Schwarzer, G., & Carpenter, J. (2008). Arcsine test for publication bias in meta-analyses with binary outcomes. Statistics in Medicine, 27(5), 746–763. https://doi.org/10.1002/sim.2971

Stanley, T. D., & Doucouliagos, H. (2014). Meta-regression approximations to reduce publication selection bias. Research Synthesis Methods, 5(1), 60–78. https://doi.org/10.1002/jrsm.1095

Sterne, J. A. C., & Egger, M. (2005). Regression methods to detect publication and other bias in meta-analysis. In H. R. Rothstein, A. J. Sutton, & M. Borenstein (Eds.) Publication bias in meta-analysis: Prevention, assessment, and adjustments (pp. 99–110). Chichester, England: Wiley.

Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://doi.org/10.18637/jss.v036.i03

Examples

### copy data into 'dat' and examine data
dat <- dat.egger2001

### calculate log odds ratios and corresponding sampling variances (but remove ISIS-4 trial)
dat <- escalc(measure="OR", ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat, subset=-16)

### fit random-effects model
res <- rma(yi, vi, data=dat)
res
#> 
#> Random-Effects Model (k = 15; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of total heterogeneity): 0.1911 (SE = 0.2106)
#> tau (square root of estimated tau^2 value):      0.4371
#> I^2 (total heterogeneity / total variability):   38.19%
#> H^2 (total variability / sampling variability):  1.62
#> 
#> Test for Heterogeneity:
#> Q(df = 14) = 20.9184, p-val = 0.1037
#> 
#> Model Results:
#> 
#> estimate      se     zval    pval    ci.lb    ci.ub      
#>  -0.8745  0.2080  -4.2049  <.0001  -1.2822  -0.4669  *** 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 

### classical Egger test
regtest(res, model="lm")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     weighted regression with multiplicative dispersion
#> Predictor: standard error
#> 
#> Test for Funnel Plot Asymmetry: t = -3.1783, df = 13, p = 0.0073
#> Limit Estimate (as sei -> 0):   b = -0.1512 (CI: -0.5130, 0.2106)
#> 

### mixed-effects meta-regression version of the Egger test
regtest(res)
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: standard error
#> 
#> Test for Funnel Plot Asymmetry: z = -2.8062, p = 0.0050
#> Limit Estimate (as sei -> 0):   b = -0.1639 (CI: -0.5681, 0.2402)
#> 

### same tests, but passing outcomes directly
regtest(yi, vi, data=dat, model="lm")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     weighted regression with multiplicative dispersion
#> Predictor: standard error
#> 
#> Test for Funnel Plot Asymmetry: t = -3.1783, df = 13, p = 0.0073
#> Limit Estimate (as sei -> 0):   b = -0.1512 (CI: -0.5130, 0.2106)
#> 
regtest(yi, vi, data=dat)
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: standard error
#> 
#> Test for Funnel Plot Asymmetry: z = -2.8062, p = 0.0050
#> Limit Estimate (as sei -> 0):   b = -0.1639 (CI: -0.5681, 0.2402)
#> 

### if dat$yi is computed with escalc(), sample size information is stored in attributes
dat$yi
#>  [1] -0.83034830 -1.05605267 -1.27833981 -0.04348511  0.22314355 -2.40751999 -1.28093385 -1.19170271
#>  [9] -0.69574796 -2.20827441 -2.03815988 -0.85015093 -0.79323064 -0.29933987 -1.57078846
#> attr(,"ni")
#>  [1]   76  270  400   94  298  115   48   43  151   54  169   56  252 2316  215
#> attr(,"measure")
#> [1] "OR"

### then this will also work
regtest(yi, vi, data=dat, predictor="ni")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: sample size
#> 
#> Test for Funnel Plot Asymmetry: z = 1.7938, p = 0.0728
#> 

### similarly when passing a model object to the function
regtest(res, model="lm", predictor="ni")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     weighted regression with multiplicative dispersion
#> Predictor: sample size
#> 
#> Test for Funnel Plot Asymmetry: t = 2.8955, df = 13, p = 0.0125
#> 
regtest(res, model="lm", predictor="ninv")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     weighted regression with multiplicative dispersion
#> Predictor: inverse of the sample size
#> 
#> Test for Funnel Plot Asymmetry: t = -2.3230, df = 13, p = 0.0370
#> Limit Estimate (as ni -> inf):  b = -0.3731 (CI: -0.6872, -0.0591)
#> 
regtest(res, predictor="ni")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: sample size
#> 
#> Test for Funnel Plot Asymmetry: z = 1.7938, p = 0.0728
#> 
regtest(res, predictor="ninv")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: inverse of the sample size
#> 
#> Test for Funnel Plot Asymmetry: z = -1.4313, p = 0.1524
#> Limit Estimate (as ni -> inf):  b = -0.5636 (CI: -1.0712, -0.0559)
#> 

### otherwise have to supply sample sizes manually
dat$yi <- c(dat$yi) # this removes the 'ni' attribute from 'yi'
dat$nitotal <- with(dat, n1i + n2i)
regtest(yi, vi, ni=nitotal, data=dat, predictor="ni")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: sample size
#> 
#> Test for Funnel Plot Asymmetry: z = 1.7938, p = 0.0728
#> 
res <- rma(yi, vi, data=dat)
regtest(res, predictor="ni", ni=nitotal, data=dat)
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: sample size
#> 
#> Test for Funnel Plot Asymmetry: z = 1.7938, p = 0.0728
#> 

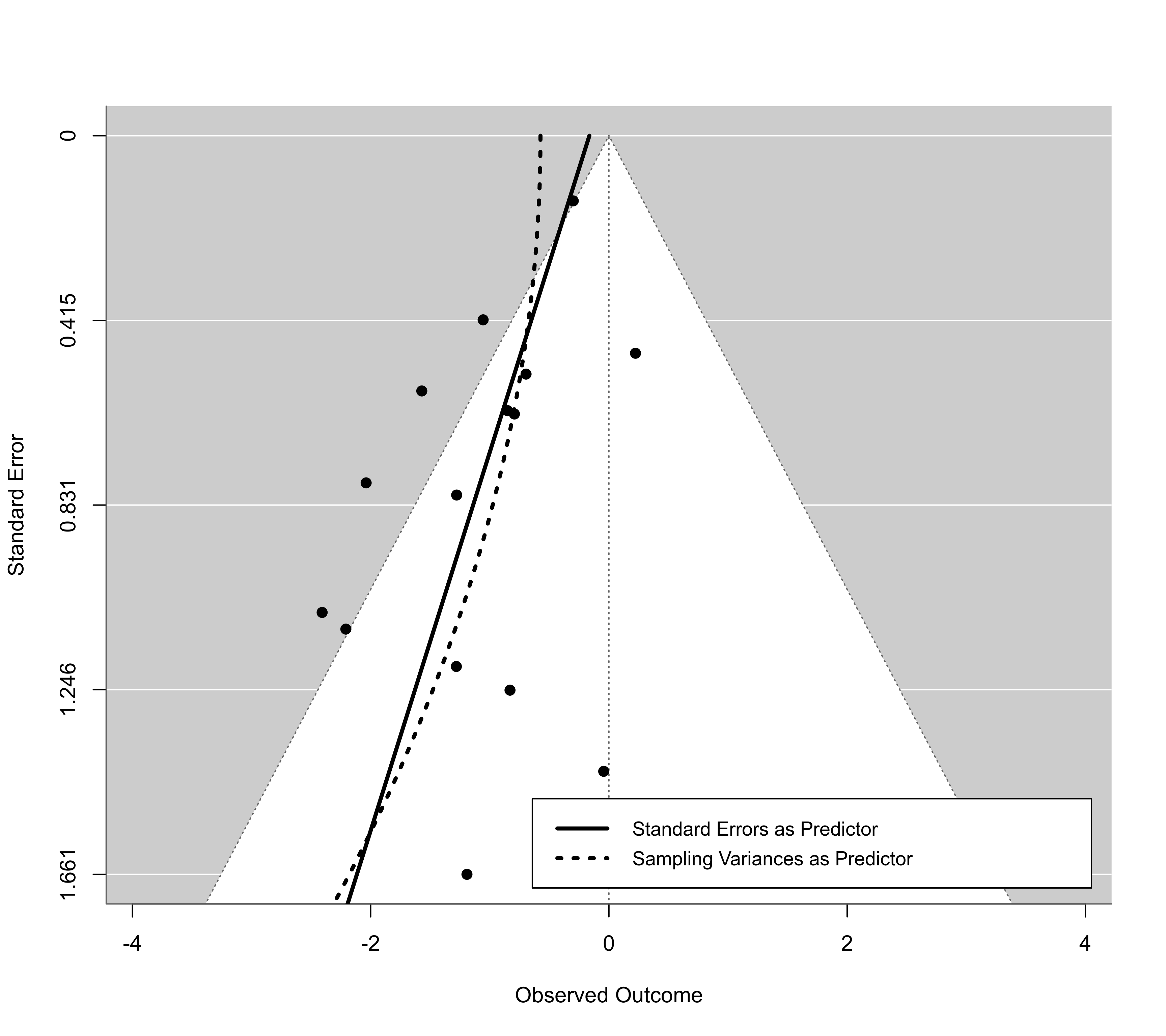
### standard funnel plot (with standard errors on the y-axis)
funnel(res, refline=0)

### regression test (by default the standard errors are used as predictor)
reg <- regtest(res)
reg
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: standard error
#> 
#> Test for Funnel Plot Asymmetry: z = -2.8062, p = 0.0050
#> Limit Estimate (as sei -> 0):   b = -0.1639 (CI: -0.5681, 0.2402)
#> 

### add regression line to funnel plot
se <- seq(0,1.8,length=100)
lines(coef(reg$fit)[1] + coef(reg$fit)[2]*se, se, lwd=3)

### regression test (using the sampling variances as predictor)
reg <- regtest(res, predictor="vi")

### add regression line to funnel plot (using the sampling variances as predictor)
lines(coef(reg$fit)[1] + coef(reg$fit)[2]*se^2, se, lwd=3, lty="dotted")

### add legend
legend("bottomright", inset=0.02, lty=c("solid","dotted"), lwd=3, cex=0.9, bg="white",
       legend=c("Standard Errors as Predictor",
                "Sampling Variances as Predictor"))


### testing for asymmetry after accounting for the influence of a moderator
res <- rma(yi, vi, mods = ~ year, data=dat)
regtest(res, model="lm")
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     weighted regression with multiplicative dispersion
#> Predictor: standard error
#> 
#> Test for Funnel Plot Asymmetry: t = -3.1057, df = 12, p = 0.0091
#> 
regtest(res)
#> 
#> Regression Test for Funnel Plot Asymmetry
#> 
#> Model:     mixed-effects meta-regression model
#> Predictor: standard error
#> 
#> Test for Funnel Plot Asymmetry: z = -2.3198, p = 0.0204
#>