Studies on the Effectiveness of Intravenous Magnesium in Acute Myocardial Infarction
dat.egger2001.RdResults from 16 trials examining the effectiveness of intravenous magnesium in the prevention of death following acute myocardial infarction.
dat.egger2001Format
The data frame contains the following columns:
| id | numeric | trial id number |
| study | character | first author or trial name |
| year | numeric | publication year |
| ai | numeric | number of deaths in the magnesium group |
| n1i | numeric | number of patients in the magnesium group |
| ci | numeric | number of deaths in the control group |
| n2i | numeric | number of patients in the control group |
Details
The dataset includes the results from 16 randomized clinical trials that examined the effectiveness of intravenous magnesium in the prevention of death following acute myocardial infarction. Studies 1-7 were included in the meta-analyses by Teo et al. (1991) and Horner (1992) and were combined with the results from the LIMIT-2 trial (Woods et al., 1992) in Yusuf et al. (1993), suggesting that magnesium is an effective treatment for reducing mortality. However, the results from the ISIS-4 mega trial (ISIS-4 Collaborative Group, 1995) indicated no reduction in mortality with magnesium treatment. Publication bias has been suggested as one possible explanation for the conflicting findings (Egger & Davey Smith, 1995).
The present dataset includes some additional trials and are based on Table 18.2 from Egger, Davey Smith, and Altman (2001).
Source
Egger, M., Davey Smith, G., & Altman, D. G. (Eds.) (2001). Systematic reviews in health care: Meta-analysis in context (2nd ed.). London: BMJ Books.
References
Egger, M., & Davey Smith, G. (1995). Misleading meta-analysis: Lessons from “an effective, safe, simple” intervention that wasn't. British Medical Journal, 310(6982), 752–754. https://doi.org/10.1136/bmj.310.6982.752
Horner, S. M. (1992). Efficacy of intravenous magnesium in acute myocardial infarction in reducing arrhythmias and mortality: Meta-analysis of magnesium in acute myocardial infarction. Circulation, 86(3), 774–779. https://doi.org/10.1161/01.cir.86.3.774
ISIS-4 Collaborative Group (1995). ISIS-4: A randomised factorial trial assessing early oral captopril, oral mononitrate, and intravenous magnesium sulphate in 58,050 patients with suspected acute myocardial infarction. Lancet, 345(8951), 669–685. https://doi.org/10.1016/S0140-6736(95)90865-X
Teo, K. K., Yusuf, S., Collins, R., Held, P. H., & Peto, R. (1991). Effects of intravenous magnesium in suspected acute myocardial infarction: Overview of randomised trials. British Medical Journal, 303(6816), 1499–1503. https://doi.org/10.1136/bmj.303.6816.1499
Woods, K. L., Fletcher, S., Roffe, C., & Haider, Y. (1992). Intravenous magnesium sulphate in suspected acute myocardial infarction: Results of the second Leicester Intravenous Magnesium Intervention Trial (LIMIT-2). Lancet, 339(8809), 1553–1558. https://doi.org/10.1016/0140-6736(92)91828-v
Yusuf, S., Teo, K., & Woods, K. (1993). Intravenous magnesium in acute myocardial infarction: An effective, safe, simple, and inexpensive treatment. Circulation, 87(6), 2043–2046. https://doi.org/10.1161/01.cir.87.6.2043
See also
Concepts
medicine, cardiology, Peto's method, publication bias
Examples
### copy data into 'dat' and examine data
dat <- dat.egger2001
dat
#> id study year ai n1i ci n2i
#> 1 1 Morton 1984 1 40 2 36
#> 2 2 Rasmussen 1986 9 135 23 135
#> 3 3 Smith 1986 2 200 7 200
#> 4 4 Abraham 1987 1 48 1 46
#> 5 5 Feldstedt 1988 10 150 8 148
#> 6 6 Shechter 1989 1 59 9 56
#> 7 7 Ceremuzynski 1989 1 25 3 23
#> 8 8 Bertschat 1989 0 22 1 21
#> 9 9 Singh 1990 6 76 11 75
#> 10 10 Pereira 1990 1 27 7 27
#> 11 11 Shechter 1991 2 89 12 80
#> 12 12 Golf 1991 5 23 13 33
#> 13 13 Thogersen 1991 4 130 8 122
#> 14 14 LIMIT-2 1992 90 1159 118 1157
#> 15 15 Shechter 1995 4 107 17 108
#> 16 16 ISIS-4 1995 2216 29011 2103 29039
### load metafor package
library(metafor)
### meta-analysis of trials 1-7 using Peto's method (as in Teo et al., 1991)
res <- rma.peto(ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat, subset=1:7)
print(res, digits=2)
#>
#> Equal-Effects Model (k = 7)
#>
#> I^2 (total heterogeneity / total variability): 21.13%
#> H^2 (total variability / sampling variability): 1.27
#>
#> Test for Heterogeneity:
#> Q(df = 6) = 7.61, p-val = 0.27
#>
#> Model Results (log scale):
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.80 0.24 -3.39 <.01 -1.26 -0.34
#>
#> Model Results (OR scale):
#>
#> estimate ci.lb ci.ub
#> 0.45 0.28 0.71
#>
### meta-analysis of trials 1-7 and LIMIT-2 (as in Yusuf et al., 1993)
res <- rma.peto(ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat, subset=c(1:7,14))
print(res, digits=2)
#>
#> Equal-Effects Model (k = 8)
#>
#> I^2 (total heterogeneity / total variability): 35.71%
#> H^2 (total variability / sampling variability): 1.56
#>
#> Test for Heterogeneity:
#> Q(df = 7) = 10.89, p-val = 0.14
#>
#> Model Results (log scale):
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.44 0.12 -3.52 <.01 -0.68 -0.19
#>
#> Model Results (OR scale):
#>
#> estimate ci.lb ci.ub
#> 0.65 0.51 0.82
#>
### meta-analysis of all trials except ISIS-4
res <- rma.peto(ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat, subset=-16)
print(res, digits=2)
#>
#> Equal-Effects Model (k = 15)
#>
#> I^2 (total heterogeneity / total variability): 36.34%
#> H^2 (total variability / sampling variability): 1.57
#>
#> Test for Heterogeneity:
#> Q(df = 14) = 21.99, p-val = 0.08
#>
#> Model Results (log scale):
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.60 0.11 -5.53 <.01 -0.81 -0.39
#>
#> Model Results (OR scale):
#>
#> estimate ci.lb ci.ub
#> 0.55 0.44 0.68
#>
predict(res, transf=exp, digits=2)
#>
#> pred ci.lb ci.ub
#> 0.55 0.44 0.68
#>
### meta-analysis of all trials including ISIS-4
res <- rma.peto(ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat)
print(res, digits=2)
#>
#> Equal-Effects Model (k = 16)
#>
#> I^2 (total heterogeneity / total variability): 73.12%
#> H^2 (total variability / sampling variability): 3.72
#>
#> Test for Heterogeneity:
#> Q(df = 15) = 55.80, p-val < .01
#>
#> Model Results (log scale):
#>
#> estimate se zval pval ci.lb ci.ub
#> 0.01 0.03 0.20 0.84 -0.05 0.07
#>
#> Model Results (OR scale):
#>
#> estimate ci.lb ci.ub
#> 1.01 0.95 1.07
#>
predict(res, transf=exp, digits=2)
#>
#> pred ci.lb ci.ub
#> 1.01 0.95 1.07
#>
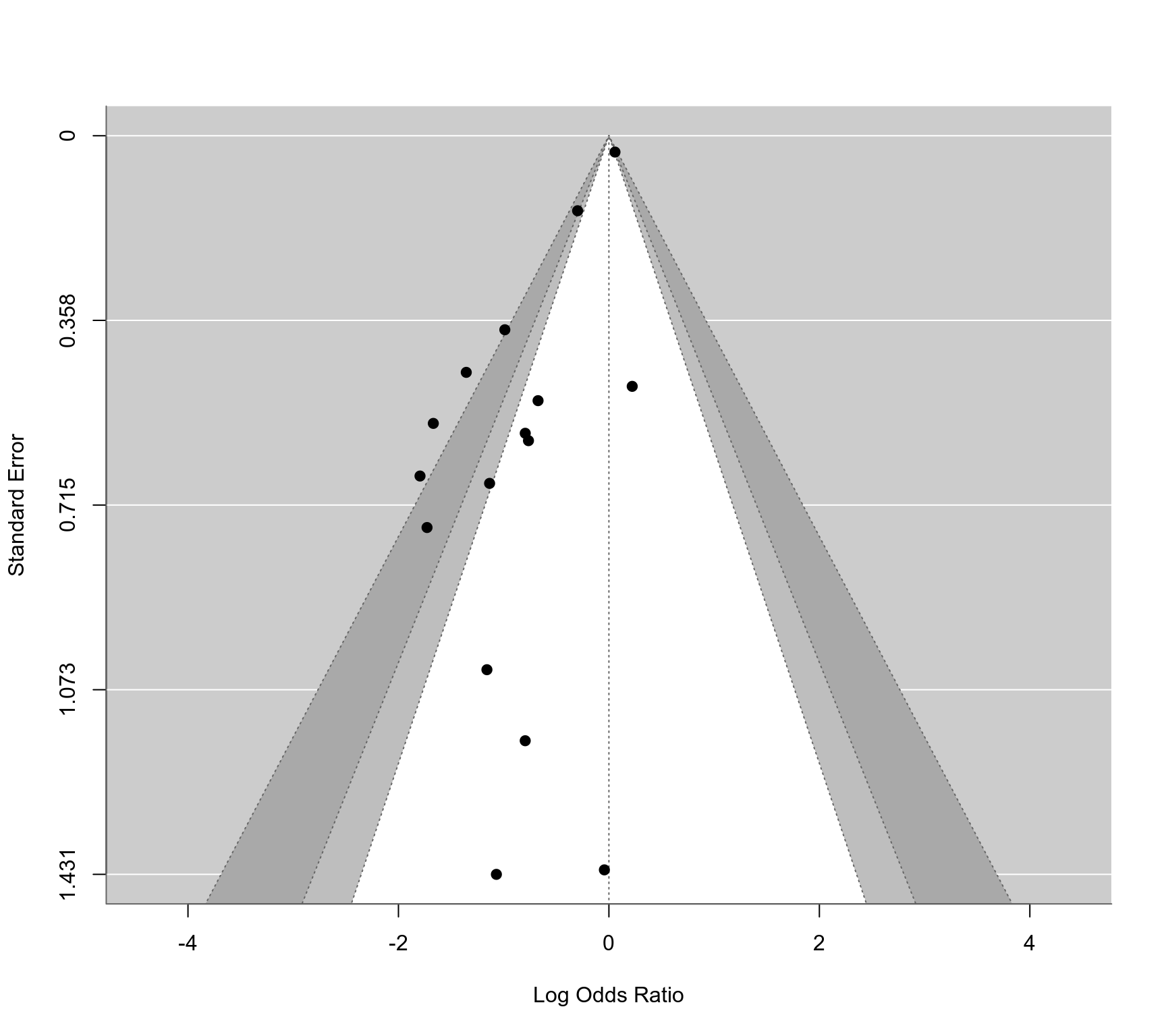
### contour-enhanced funnel plot centered at 0
funnel(res, refline=0, level=c(90, 95, 99), shade=c("white", "gray", "darkgray"))