Profile Likelihood Plots for 'rma' Objects

Functions to profile the (restricted) log-likelihood for objects of class "rma.uni", "rma.mv", "rma.uni.selmodel", and "rma.ls".

# S3 method for class 'rma.uni'
profile(fitted, xlim, ylim, steps=20, lltol=1e-03,
        progbar=TRUE, parallel="no", ncpus=1, cl, plot=TRUE, ...)

# S3 method for class 'rma.mv'
profile(fitted, sigma2, tau2, rho, gamma2, phi, xlim, ylim, steps=20, lltol=1e-03,
        progbar=TRUE, parallel="no", ncpus=1, cl, plot=TRUE, ...)

# S3 method for class 'rma.uni.selmodel'
profile(fitted, tau2, delta, xlim, ylim, steps=20, lltol=1e-03,
        progbar=TRUE, parallel="no", ncpus=1, cl, plot=TRUE, ...)

# S3 method for class 'rma.ls'
profile(fitted, alpha, xlim, ylim, steps=20, lltol=1e-03,
        progbar=TRUE, parallel="no", ncpus=1, cl, plot=TRUE, ...)

# S3 method for class 'profile.rma'
print(x, ...)
# S3 method for class 'profile.rma'
plot(x, xlim, ylim, pch=19, xlab, ylab, main, refline=TRUE, cline=FALSE, ...)

Arguments

fitted: an object of class "rma.uni", "rma.mv", "rma.uni.selmodel", or "rma.ls".
x: an object of class "profile.rma" (for plot and print).
sigma2: optional integer to specify for which \(\sigma^2\) parameter the likelihood should be profiled.
tau2: optional integer to specify for which \(\tau^2\) parameter the likelihood should be profiled.
rho: optional integer to specify for which \(\rho\) parameter the likelihood should be profiled.
gamma2: optional integer to specify for which \(\gamma^2\) parameter the likelihood should be profiled.
phi: optional integer to specify for which \(\phi\) parameter the likelihood should be profiled.
delta: optional integer to specify for which \(\delta\) parameter the likelihood should be profiled.
alpha: optional integer to specify for which \(\alpha\) parameter the likelihood should be profiled.
xlim: optional vector to specify the lower and upper limit of the parameter over which the profiling should be done. If unspecified, the function sets these limits automatically.
ylim: optional vector to specify the y-axis limits when plotting the profiled likelihood. If unspecified, the function sets these limits automatically.
steps: number of points between xlim[1] and xlim[2] (inclusive) for which the likelihood should be evaluated (the default is 20). Can also be a numeric vector of length 2 or longer to specify for which parameter values the likelihood should be evaluated (in this case, xlim is automatically set to range(steps) if unspecified).
lltol: numerical tolerance used when comparing values of the profiled log-likelihood with the log-likelihood of the fitted model (the default is 1e-03).
progbar: logical to specify whether a progress bar should be shown (the default is TRUE).
parallel: character string to specify whether parallel processing should be used (the default is "no"). For parallel processing, set to either "snow" or "multicore". See ‘Details’.
ncpus: integer to specify the number of processes to use in the parallel processing.
cl: optional cluster to use if parallel="snow". If unspecified, a cluster on the local machine is created for the duration of the call.
plot: logical to specify whether the profile plot should be drawn after profiling is finished (the default is TRUE).
pch: plotting symbol to use. By default, a filled circle is used. See points for other options.
refline: logical to specify whether the value of the parameter estimate should be indicated by a dotted vertical line and its log-likelihood value by a dotted horizontal line (the default is TRUE).
cline: logical to specify whether a horizontal reference line should be added to the plot that indicates the log-likelihood value corresponding to the 95% profile confidence interval (the default is FALSE). Can also be a numeric value between 0 and 100 to specify the confidence interval level.
xlab: title for the x-axis. If unspecified, the function sets an appropriate axis title.
ylab: title for the y-axis. If unspecified, the function sets an appropriate axis title.
main: title for the plot. If unspecified, the function sets an appropriate title.
...: other arguments.

Details

The function fixes a particular parameter of the model and then computes the maximized (restricted) log-likelihood over the remaining parameters of the model. By fixing the parameter of interest to a range of values, a profile of the (restricted) log-likelihood is constructed.

Selecting the Parameter(s) to Profile

The parameters that can be profiled depend on the model object:

For objects of class "rma.uni" obtained with the rma.uni function, the function profiles over \(\tau^2\) (not for equal-effects models).
For objects of class "rma.mv" obtained with the rma.mv function, profiling is done by default over all variance and correlation components of the model. Alternatively, one can use the sigma2, tau2, rho, gamma2, or phi arguments to specify over which parameter the profiling should be done. Only one of these arguments can be used at a time. A single integer is used to specify the number of the parameter.
For selection model objects of class "rma.uni.selmodel" obtained with the selmodel function, profiling is done by default over \(\tau^2\) (for models where this is an estimated parameter) and all selection model parameters. Alternatively, one can choose to profile only \(\tau^2\) by setting tau2=TRUE or one can select one of the selection model parameters to profile by specifying its number via the delta argument.
For location-scale model objects of class "rma.ls" obtained with the rma.uni function, profiling is done by default over all \(\alpha\) parameters that are part of the scale model. Alternatively, one can select one of the parameters to profile by specifying its number via the alpha argument.

Interpreting Profile Likelihood Plots

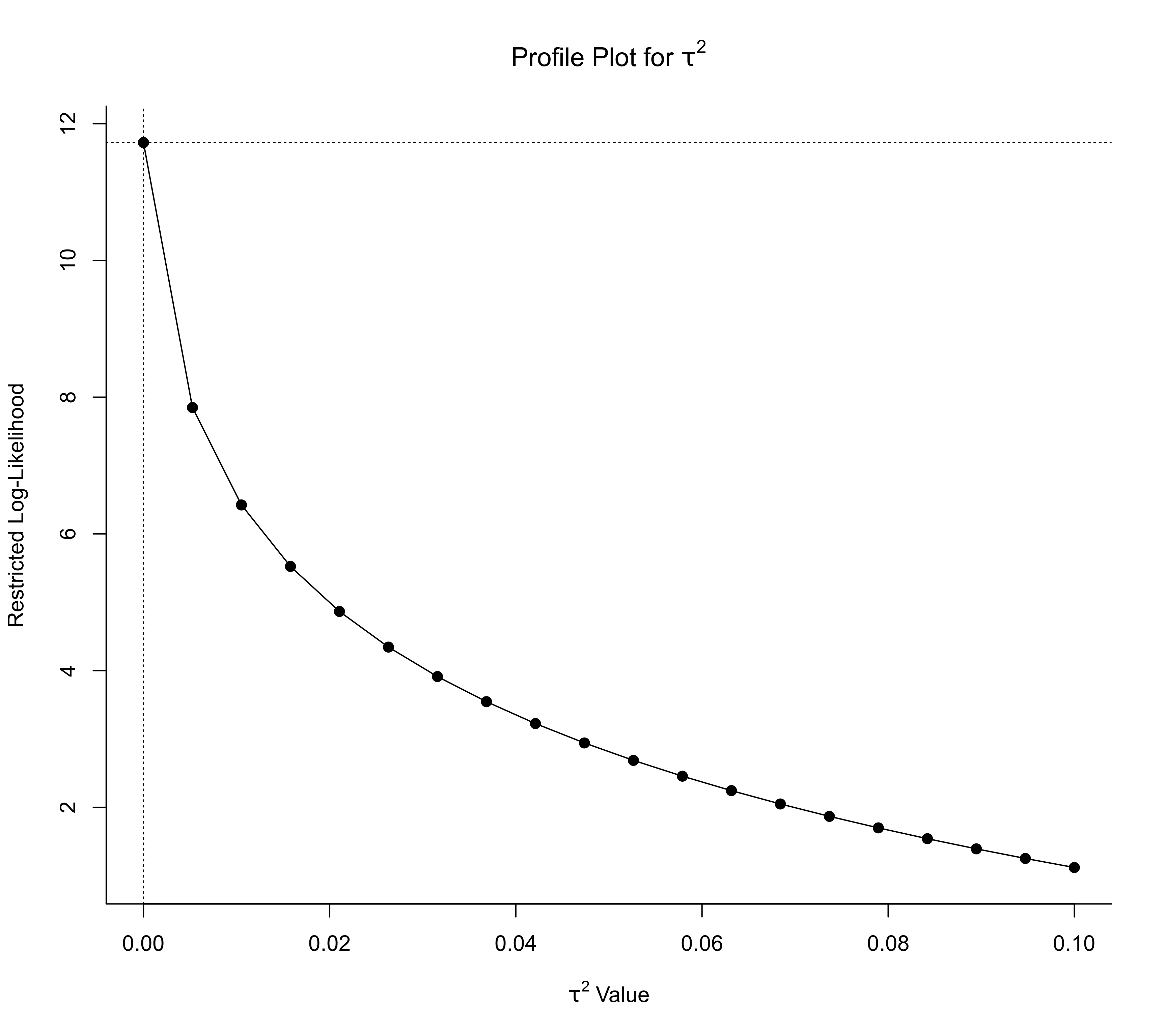
A profile likelihood plot should show a single peak at the corresponding ML/REML estimate. If refline=TRUE (the default), the value of the parameter estimate is indicated by a dotted vertical line and its log-likelihood value by a dotted horizontal line. Hence, the intersection of these two lines should correspond to the peak (assuming that the model was fitted with ML/REML estimation).

When profiling a variance component (or some other parameter that cannot be negative), the peak may be at zero (if this corresponds to the ML/REML estimate of the parameter). In this case, the profiled log-likelihood should be a monotonically decreasing function of the parameter. Similarly, when profiling a correlation component, the peak may be at -1 or +1.

If the profiled log-likelihood has multiple peaks, this indicates that the likelihood surface is not unimodal. In such cases, the ML/REML estimate may correspond to a local optimum (when the intersection of the two dotted lines is not at the highest peak).

If the profile is flat (over the entire parameter space or large portions of it), then this suggests that at least some of the parameters of the model are not identifiable (and the parameter estimates obtained are to some extent arbitrary). See Raue et al. (2009) for some further discussion of parameter identifiability and the use of profile likelihoods to check for this.

The function checks whether any profiled log-likelihood value is actually larger than the log-likelihood of the fitted model (using a numerical tolerance of lltol). If so, a warning is issued as this might indicate that the optimizer did not identify the actual ML/REML estimate of the parameter profiled.

Parallel Processing

Profiling requires repeatedly refitting the model, which can be slow when \(k\) is large and/or the model is complex (the latter especially applies to "rma.mv" objects and also to certain "rma.uni.selmodel" or "rma.ls" objects). On machines with multiple cores, one can try to speed things up by delegating the model fitting to separate worker processes, that is, by setting parallel="snow" or parallel="multicore" and ncpus to some value larger than 1. Parallel processing makes use of the parallel package, using the makePSOCKcluster and parLapply functions when parallel="snow" or using mclapply when parallel="multicore" (the latter only works on Unix/Linux-alikes). With parallel::detectCores(), one can check on the number of available cores on the local machine.

Value

An object of class "profile.rma". The object is a list (or list of such lists) containing the following components:

One of the following (depending on the parameter that was actually profiled):

sigma2: values of \(\sigma^2\) over which the likelihood was profiled.
tau2: values of \(\tau^2\) over which the likelihood was profiled.
rho: values of \(\rho\) over which the likelihood was profiled.
gamma2: values of \(\gamma^2\) over which the likelihood was profiled.
phi: values of \(\phi\) over which the likelihood was profiled.
delta: values of \(\delta\) over which the likelihood was profiled.
alpha: values of \(\alpha\) over which the likelihood was profiled.

In addition, the following components are included:

ll: (restricted) log-likelihood values at the corresponding parameter values.
beta: a matrix with the estimated model coefficients at the corresponding parameter values.
ci.lb: a matrix with the lower confidence interval bounds of the model coefficients at the corresponding parameter values.
ci.ub: a matrix with the upper confidence interval bounds of the model coefficients at the corresponding parameter values.
...: some additional elements/values.

Note that the list is returned invisibly.

Author

Wolfgang Viechtbauer (wvb@metafor-project.org, https://www.metafor-project.org).

References

Raue, A., Kreutz, C., Maiwald, T., Bachmann, J., Schilling, M., Klingmuller, U., & Timmer, J. (2009). Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics, 25(15), 1923–1929. https://doi.org/10.1093/bioinformatics/btp358

Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://doi.org/10.18637/jss.v036.i03

Viechtbauer, W., & López-López, J. A. (2022). Location-scale models for meta-analysis. Research Synthesis Methods. 13(6), 697–715. https://doi.org/10.1002/jrsm.1562

Examples

### calculate log odds ratios and corresponding sampling variances
dat <- escalc(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg)

### fit random-effects model using rma.uni()
res <- rma(yi, vi, data=dat)

### profile over tau^2
profile(res, progbar=FALSE)


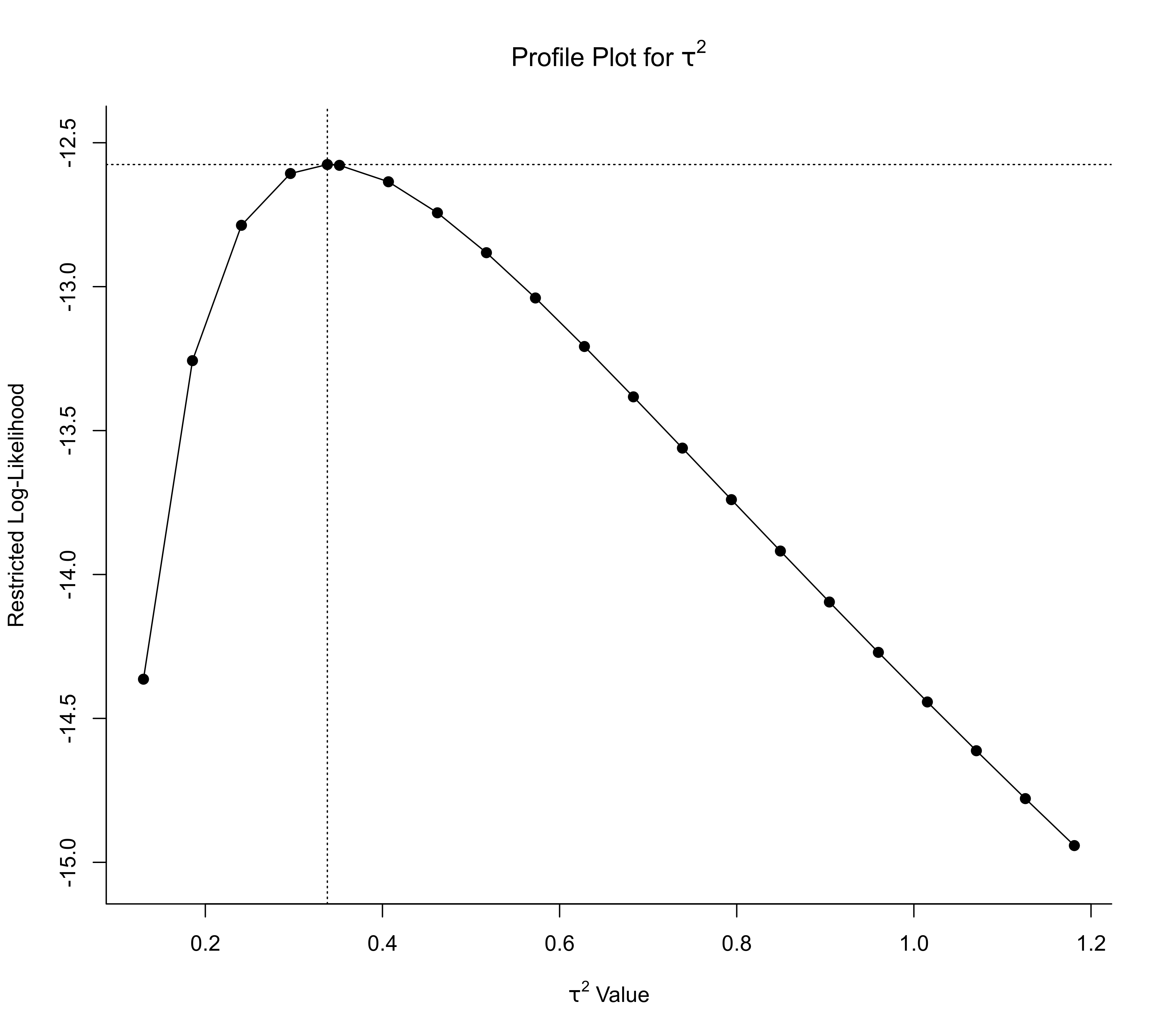### adjust xlim
profile(res, progbar=FALSE, xlim=c(0,1))


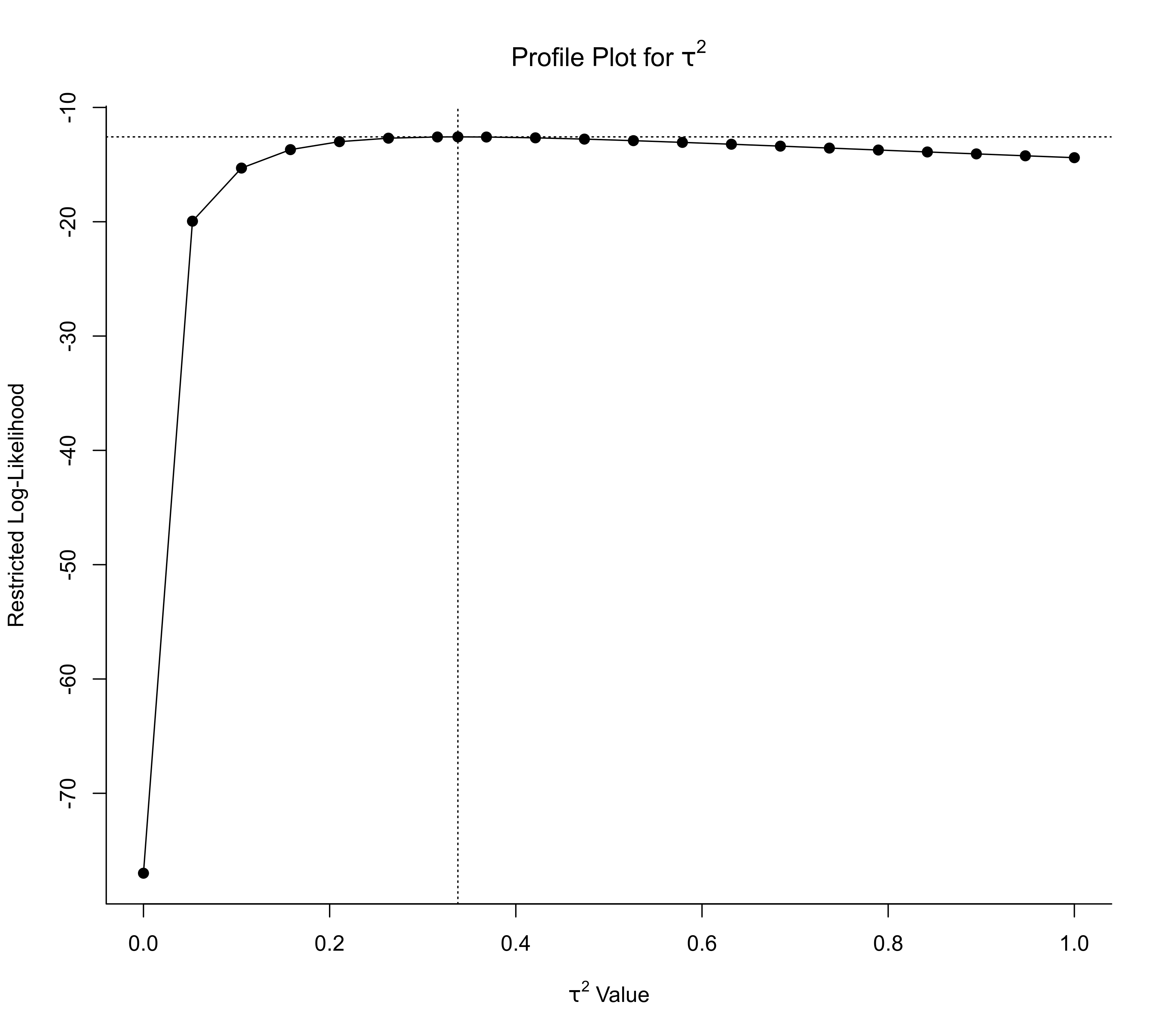### specify tau^2 values at which to profile the likelihood
profile(res, progbar=FALSE, steps=c(seq(0,0.2,length=20),seq(0.3,1,by=0.1)))


### change data into long format
dat.long <- to.long(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg, append=FALSE)

### set levels/labels for group ("con" = control/non-vaccinated, "exp" = experimental/vaccinated)
dat.long$group <- factor(dat.long$group, levels=c(2,1), labels=c("con","exp"))

### calculate log odds and corresponding sampling variances
dat.long <- escalc(measure="PLO", xi=out1, mi=out2, data=dat.long)
dat.long
#> 
#>    study group out1  out2      yi     vi 
#> 1      1   exp    4   119 -3.3928 0.2584 
#> 2      1   con   11   128 -2.4541 0.0987 
#> 3      2   exp    6   300 -3.9120 0.1700 
#> 4      2   con   29   274 -2.2458 0.0381 
#> 5      3   exp    3   228 -4.3307 0.3377 
#> 6      3   con   11   209 -2.9444 0.0957 
#> 7      4   exp   62 13536 -5.3860 0.0162 
#> 8      4   con  248 12619 -3.9295 0.0041 
#> 9      5   exp   33  5036 -5.0279 0.0305 
#> 10     5   con   47  5761 -4.8087 0.0215 
#> 11     6   exp  180  1361 -2.0230 0.0063 
#> 12     6   con  372  1079 -1.0649 0.0036 
#> 13     7   exp    8  2537 -5.7593 0.1254 
#> 14     7   con   10   619 -4.1255 0.1016 
#> 15     8   exp  505 87886 -5.1592 0.0020 
#> 16     8   con  499 87892 -5.1713 0.0020 
#> 17     9   exp   29  7470 -5.5514 0.0346 
#> 18     9   con   45  7232 -5.0796 0.0224 
#> 19    10   exp   17  1699 -4.6046 0.0594 
#> 20    10   con   65  1600 -3.2034 0.0160 
#> 21    11   exp  186 50448 -5.6030 0.0054 
#> 22    11   con  141 27197 -5.2621 0.0071 
#> 23    12   exp    5  2493 -6.2118 0.2004 
#> 24    12   con    3  2338 -6.6584 0.3338 
#> 25    13   exp   27 16886 -6.4384 0.0371 
#> 26    13   con   29 17825 -6.4211 0.0345 
#> 

### fit bivariate random-effects model using rma.mv()
res <- rma.mv(yi, vi, mods = ~ group, random = ~ group | study, struct="UN", data=dat.long)
res
#> 
#> Multivariate Meta-Analysis Model (k = 26; method: REML)
#> 
#> Variance Components:
#> 
#> outer factor: study (nlvls = 13)
#> inner factor: group (nlvls = 2)
#> 
#>             estim    sqrt  k.lvl  fixed  level 
#> tau^2.1    2.6173  1.6178     13     no    con 
#> tau^2.2    1.5486  1.2444     13     no    exp 
#> 
#>      rho.con  rho.exp    con  exp 
#> con        1               -   13 
#> exp   0.9450        1     no    - 
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 24) = 5270.3863, p-val < .0001
#> 
#> Test of Moderators (coefficient 2):
#> QM(df = 1) = 15.5470, p-val < .0001
#> 
#> Model Results:
#> 
#>           estimate      se     zval    pval    ci.lb    ci.ub      
#> intrcpt    -4.0960  0.4529  -9.0432  <.0001  -4.9837  -3.2082  *** 
#> groupexp   -0.7414  0.1880  -3.9430  <.0001  -1.1099  -0.3729  *** 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 

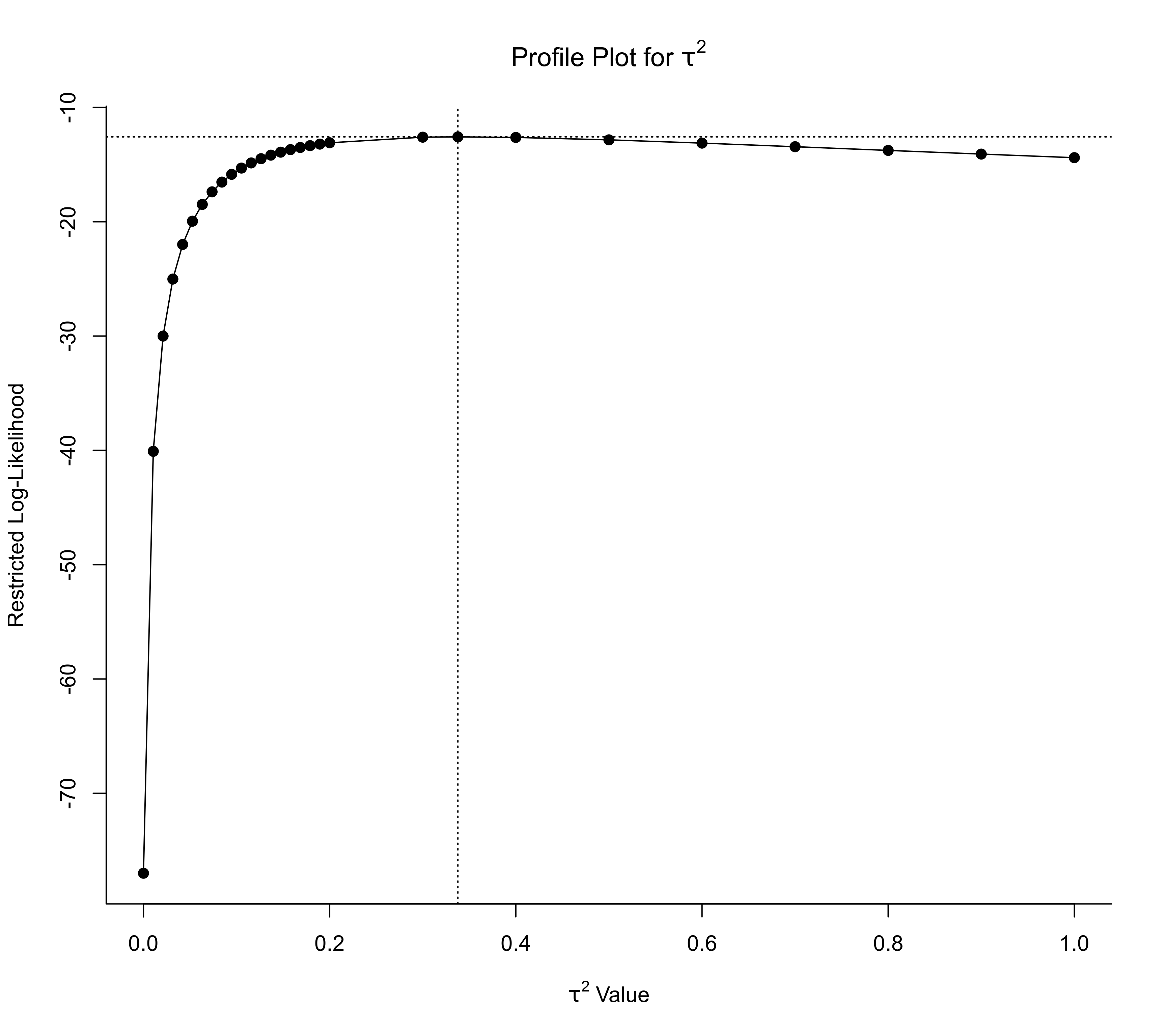
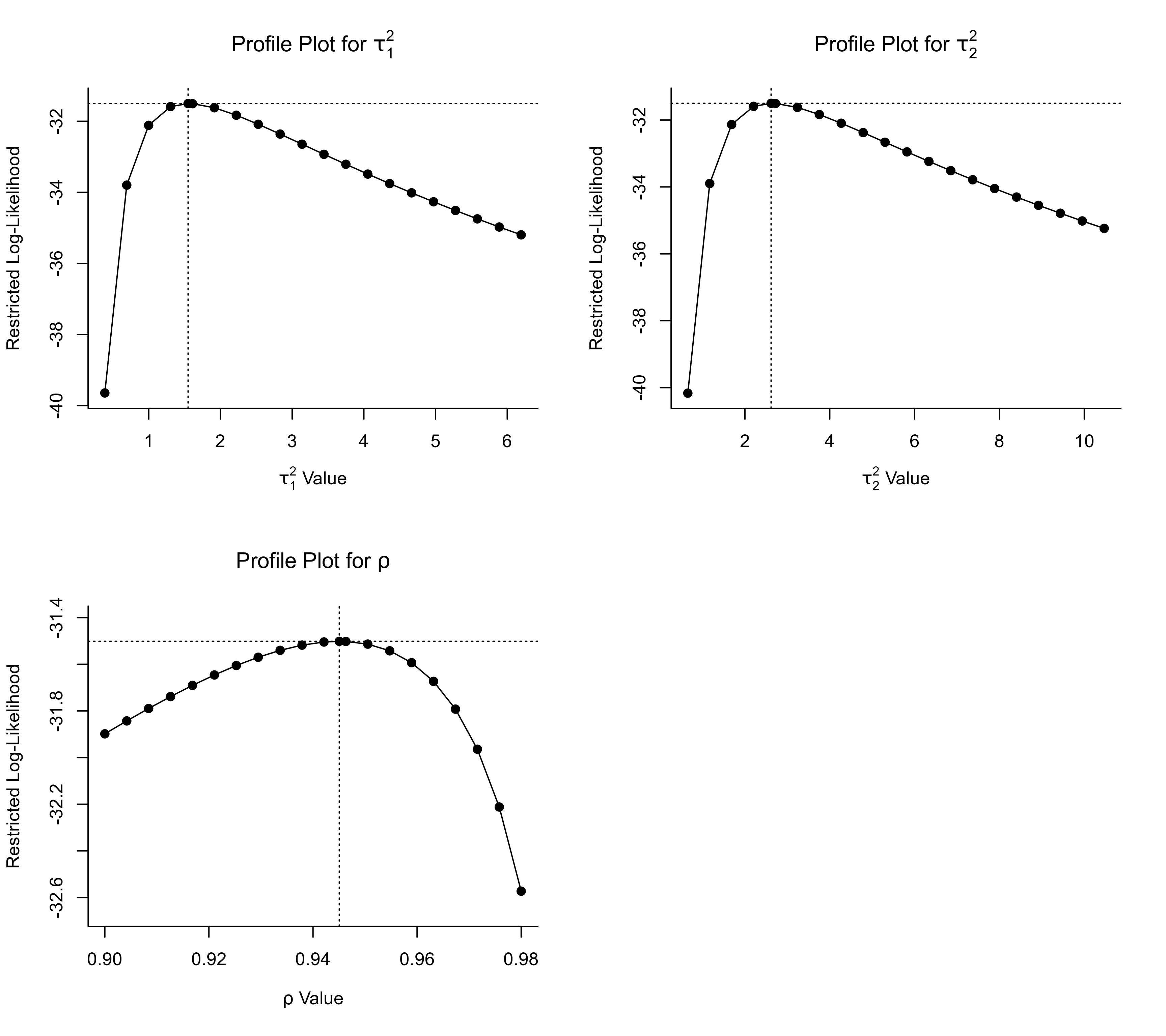
### profile over tau^2_1, tau^2_2, and rho
### note: for rho, adjust region over which profiling is done ('zoom in' on area around estimate)
par(mfrow=c(2,2))
profile(res, tau2=1)
profile(res, tau2=2)
profile(res, rho=1, xlim=c(0.90, 0.98))
par(mfrow=c(1,1))


### an example where the peak of the likelihood profile is at 0
dat <- escalc(measure="RD", n1i=n1i, n2i=n2i, ai=ai, ci=ci, data=dat.hine1989)
res <- rma(yi, vi, data=dat)
profile(res, progbar=FALSE)