Radial Plots for 'rma' Objects
radial.RdFunction to create radial plots for objects of class "rma".
radial(x, ...)
# S3 method for class 'rma'
radial(x, center=FALSE, xlim, zlim, xlab, zlab,
atz, aty, steps=7, level=x$level, digits=2,
transf, targs, pch=21, col, bg, back, arc.res=100,
cex, cex.lab, cex.axis, ...)Arguments
- x
an object of class
"rma".- center
logical to specify whether the plot should be centered horizontally at the model estimate (the default is
FALSE).- xlim
x-axis limits. If unspecified, the function sets the x-axis limits to some sensible values.
- zlim
z-axis limits. If unspecified, the function sets the z-axis limits to some sensible values (note that the z-axis limits are the actual vertical limit of the plotting region).
- xlab
title for the x-axis. If unspecified, the function sets an appropriate axis title.
- zlab
title for the z-axis. If unspecified, the function sets an appropriate axis title.
- atz
position for the z-axis tick marks and labels. If unspecified, these values are set by the function.
- aty
position for the y-axis tick marks and labels. If unspecified, these values are set by the function.
- steps
the number of tick marks for the y-axis (the default is 7). Ignored when argument
atyis used.- level
numeric value between 0 and 100 to specify the level of the z-axis error region. The default is to take the value from the object.
- digits
integer to specify the number of decimal places to which the tick mark labels of the y-axis should be rounded (the default is 2).
- transf
argument to specify a function to transform the y-axis labels (e.g.,
transf=exp; see also transf). If unspecified, no transformation is used.- targs
optional arguments needed by the function specified via
transf.- pch
plotting symbol. By default, an open circle is used. See
pointsfor other options.- col
character string to specify the (border) color of the points.
- bg
character string to specify the background color of open plot symbols.
- back
character string to specify the background color of the z-axis error region. If unspecified, a shade of gray is used. Set to
NAto suppress shading of the region.- arc.res
integer to specify the number of line segments (i.e., the resolution) when drawing the y-axis and confidence interval arcs (the default is 100).
- cex
symbol expansion factor.
- cex.lab
character expansion factor for axis labels.
- cex.axis
character expansion factor for axis annotations.
- ...
other arguments.
Details
Radial plots (also sometimes called Galbraith plots) were introduced by Galbraith (1988a, 1988b, 1994) as a way to plot estimates with different precisions. In meta-analyses, they are an interesting alternative to forest plots, especially when the number of observed effect sizes or outcomes is large (in which case the forest plot would be very large).
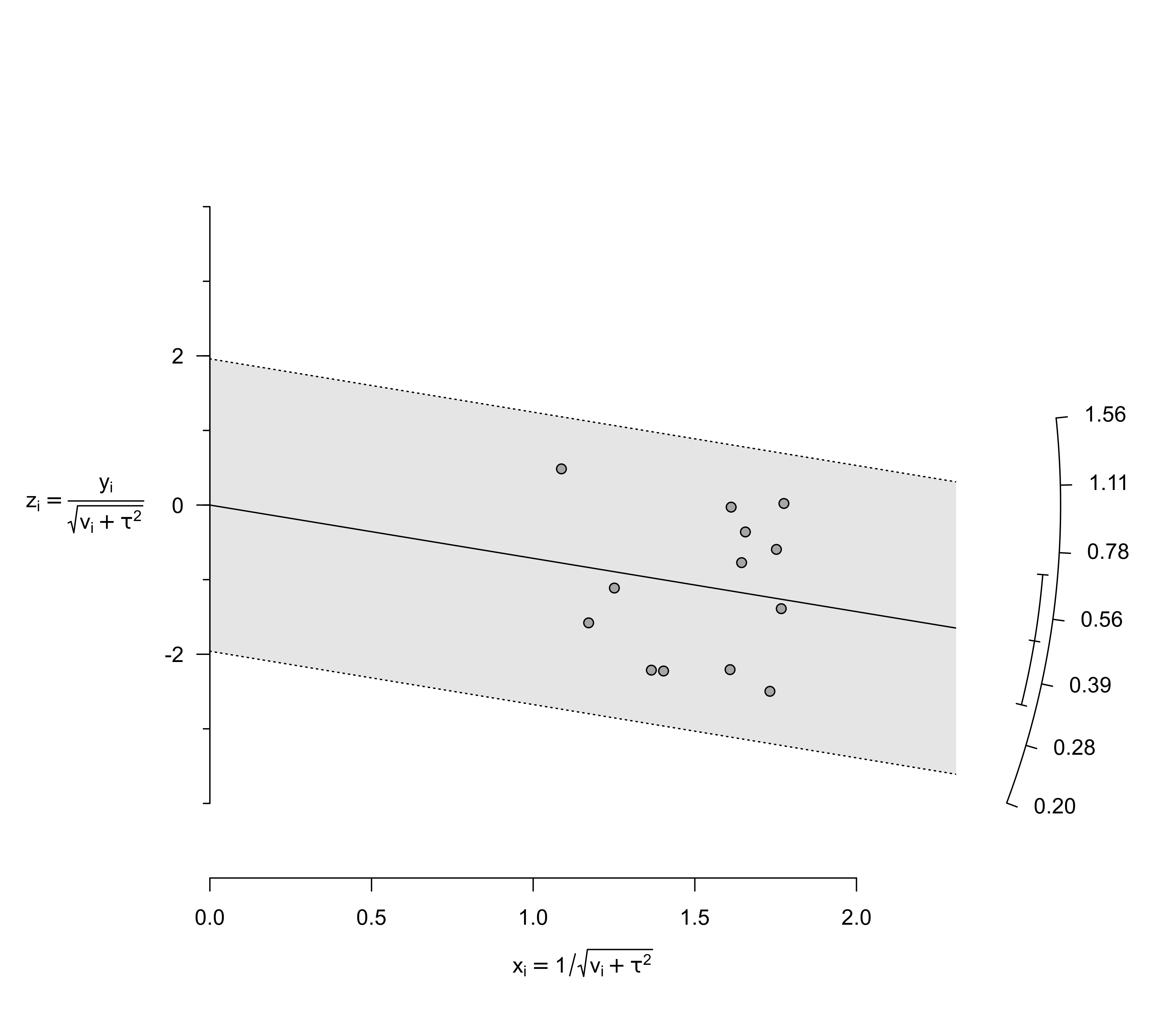
For an equal-effects model, the plot shows the inverse of the standard errors on the horizontal axis (i.e., \(1/\sqrt{v_i}\), where \(v_i\) is the sampling variance of the observed effect size or outcome) against the observed effect sizes or outcomes standardized by their corresponding standard errors on the vertical axis (i.e., \(y_i/\sqrt{v_i}\)). Since the vertical axis corresponds to standardized values, it is referred to as the z-axis within this function. On the right hand side of the plot, an arc is drawn (referred to as the y-axis within this function) corresponding to the observed effect sizes or outcomes. A line projected from (0,0) through a particular point within the plot onto this arc indicates the value of the observed effect size or outcome for that point.
For a random-effects model, the function uses \(1/\sqrt{v_i + \tau^2}\) for the horizontal axis, where \(\tau^2\) is the amount of heterogeneity as estimated based on the model. For the z-axis, \(y_i/\sqrt{v_i + \tau^2}\) is used to compute standardized values of the observed effect sizes or outcomes.
The second (inner/smaller) arc that is drawn on the right hand side indicates the model estimate (in the middle of the arc) and the corresponding confidence interval (at the ends of the arc).
The shaded region in the plot is the z-axis error region. For level=95 (or if this was the level value when the model was fitted), this corresponds to z-axis values equal to \(\pm 1.96\). Under the assumptions of the equal/random-effects models, approximately 95% of the points should fall within this region.
When center=TRUE, the values on the y-axis are centered around the model estimate. As a result, the plot is centered horizontally at the model estimate.
If the z-axis label on the left is too close to the actual z-axis and/or the arc on the right is clipped, then this can be solved by increasing the margins on the right and/or left (see par and in particular the mar argument).
Note that radial plots cannot be drawn for models that contain moderators.
Value
A data frame with components:
- x
the x-axis coordinates of the points that were plotted.
- y
the y-axis coordinates of the points that were plotted.
- ids
the study id numbers.
- slab
the study labels.
Note that the data frame is returned invisibly.
References
Galbraith, R. F. (1988a). Graphical display of estimates having differing standard errors. Technometrics, 30(3), 271–281. https://doi.org/10.1080/00401706.1988.10488400
Galbraith, R. F. (1988b). A note on graphical presentation of estimated odds ratios from several clinical trials. Statistics in Medicine, 7(8), 889–894. https://doi.org/10.1002/sim.4780070807
Galbraith, R. F (1994). Some applications of radial plots. Journal of the American Statistical Association, 89(428), 1232–1242. https://doi.org/10.1080/01621459.1994.10476864
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://doi.org/10.18637/jss.v036.i03
See also
Examples
### calculate log risk ratios and corresponding sampling variances
dat <- escalc(measure="RR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg)
dat
#>
#> trial author year tpos tneg cpos cneg ablat alloc yi vi
#> 1 1 Aronson 1948 4 119 11 128 44 random -0.8893 0.3256
#> 2 2 Ferguson & Simes 1949 6 300 29 274 55 random -1.5854 0.1946
#> 3 3 Rosenthal et al 1960 3 228 11 209 42 random -1.3481 0.4154
#> 4 4 Hart & Sutherland 1977 62 13536 248 12619 52 random -1.4416 0.0200
#> 5 5 Frimodt-Moller et al 1973 33 5036 47 5761 13 alternate -0.2175 0.0512
#> 6 6 Stein & Aronson 1953 180 1361 372 1079 44 alternate -0.7861 0.0069
#> 7 7 Vandiviere et al 1973 8 2537 10 619 19 random -1.6209 0.2230
#> 8 8 TPT Madras 1980 505 87886 499 87892 13 random 0.0120 0.0040
#> 9 9 Coetzee & Berjak 1968 29 7470 45 7232 27 random -0.4694 0.0564
#> 10 10 Rosenthal et al 1961 17 1699 65 1600 42 systematic -1.3713 0.0730
#> 11 11 Comstock et al 1974 186 50448 141 27197 18 systematic -0.3394 0.0124
#> 12 12 Comstock & Webster 1969 5 2493 3 2338 33 systematic 0.4459 0.5325
#> 13 13 Comstock et al 1976 27 16886 29 17825 33 systematic -0.0173 0.0714
#>
### fit equal-effects model
res <- rma(yi, vi, data=dat, method="EE")
### draw radial plot
radial(res)
### the line from (0,0) with a slope equal to the log risk ratio from the 4th study points
### to the corresponding effect size value on the arc (i.e., -1.44)
abline(a=0, b=dat$yi[4], lty="dotted")
 dat$yi[4]
#> [1] -1.441551
### meta-analysis of the log risk ratios using a random-effects model
res <- rma(yi, vi, data=dat)
### draw radial plot
radial(res)
dat$yi[4]
#> [1] -1.441551
### meta-analysis of the log risk ratios using a random-effects model
res <- rma(yi, vi, data=dat)
### draw radial plot
radial(res)
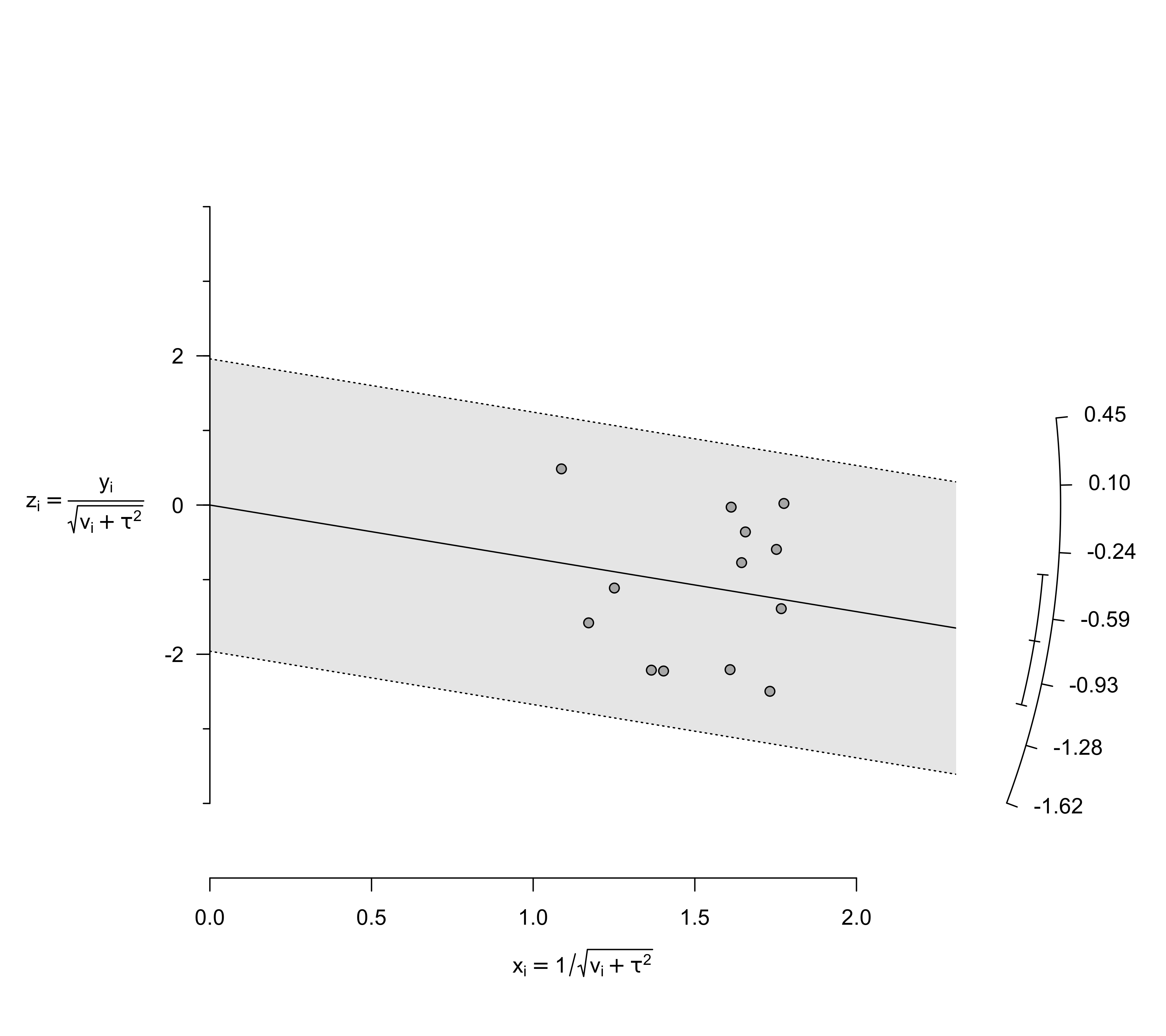 ### center the values around the model estimate
radial(res, center=TRUE)
### center the values around the model estimate
radial(res, center=TRUE)
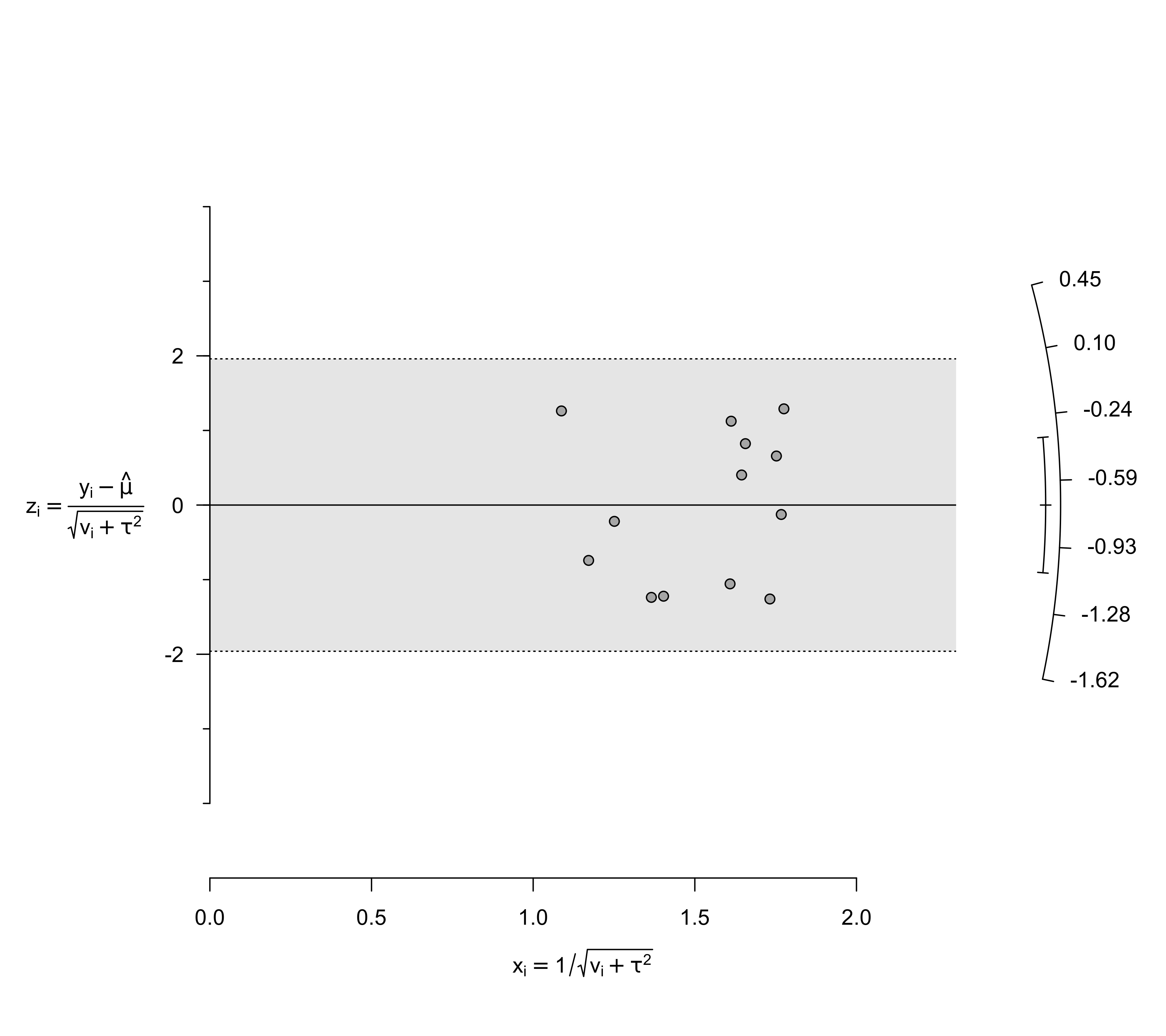 ### show risk ratio values on the y-axis arc
radial(res, transf=exp)
### show risk ratio values on the y-axis arc
radial(res, transf=exp)