Permutation Tests for 'rma.uni' Objects

Function to carry out permutation tests for objects of class "rma.uni" and "rma.ls".

permutest(x, ...)

# S3 method for class 'rma.uni'
permutest(x, exact=FALSE, iter=1000, btt=x$btt,
          permci=FALSE, progbar=TRUE, digits, control, ...)

# S3 method for class 'rma.ls'
permutest(x, exact=FALSE, iter=1000, btt=x$btt, att=x$att,
          progbar=TRUE, digits, control, ...)

Arguments

x: an object of class "rma.uni" or "rma.ls".
exact: logical to specify whether an exact permutation test should be carried out (the default is FALSE). See ‘Details’.
iter: integer to specify the number of iterations for the permutation test when not doing an exact test (the default is 1000).
btt: optional vector of indices (or list thereof) to specify which coefficients should be included in the Wald-type test. Can also be a string to grep for.
att: optional vector of indices (or list thereof) to specify which scale coefficients should be included in the Wald-type test. Can also be a string to grep for.
permci: logical to specify whether permutation-based confidence intervals (CIs) should also be constructed (the default is FALSE). Can also be a vector of indices to specify for which coefficients a permutation-based CI should be obtained.
progbar: logical to specify whether a progress bar should be shown (the default is TRUE).
digits: optional integer to specify the number of decimal places to which the printed results should be rounded. If unspecified, the default is to take the value from the object.
control: list of control values for numerical comparisons (comptol) and for uniroot (i.e., tol and maxiter). The latter is only relevant when permci=TRUE. See ‘Note’.
...: other arguments.

Details

For models without moderators, the permutation test is carried out by permuting the signs of the observed effect sizes or outcomes. The (two-sided) p-value of the permutation test is then equal to the proportion of times that the absolute value of the test statistic under the permuted data is as extreme or more extreme than under the actually observed data. See Follmann and Proschan (1999) for more details.

For models with moderators, the permutation test is carried out by permuting the rows of the model matrix (i.e., $X$). The (two-sided) p-value for a particular model coefficient is then equal to the proportion of times that the absolute value of the test statistic for the coefficient under the permuted data is as extreme or more extreme than under the actually observed data. Similarly, for the omnibus test, the p-value is the proportion of times that the test statistic for the omnibus test is as extreme or more extreme than the actually observed one (argument btt can be used to specify which coefficients should be included in this test). See Higgins and Thompson (2004) and Viechtbauer et al. (2015) for more details.

Exact versus Approximate Permutation Tests

If exact=TRUE, the function will try to carry out an exact permutation test. An exact permutation test requires fitting the model to each possible permutation. However, the number of possible permutations increases rapidly with the number of outcomes/studies (i.e., $k$). For models without moderators, there are $2^k$ possible permutations of the signs. Therefore, for $k=5$, there are 32 possible permutations, for $k=10$, there are already 1024, and for $k=20$, there are over one million such permutations.

For models with moderators, the increase in the number of possible permutations is even more severe. The total number of possible permutations of the model matrix is $k!$. Therefore, for $k=5$, there are 120 possible permutations, for $k=10$, there are 3,628,800, and for $k=20$, there are over $10^{18}$ permutations of the model matrix.

Therefore, going through all possible permutations may become infeasible. Instead of using an exact permutation test, one can set exact=FALSE (which is also the default). In that case, the function approximates the exact permutation-based p-value(s) by going through a smaller number (as specified by the iter argument) of random permutations. Therefore, running the function twice on the same data can yield (slightly) different p-values. Setting iter sufficiently large ensures that the results become stable. For full reproducibility, one can also set the seed of the random number generator before running the function (see ‘Examples’). Note that if exact=FALSE and iter is actually larger than the number of iterations required for an exact permutation test, then an exact test will automatically be carried out.

For models with moderators, the exact permutation test actually only requires fitting the model to each unique permutation of the model matrix. The number of unique permutations will be smaller than $k!$ when the model matrix contains recurring rows. This may be the case when only including categorical moderators (i.e., factors) in the model or when any quantitative moderators included in the model can only take on a small number of unique values. When exact=TRUE, the function therefore uses an algorithm to restrict the test to only the unique permutations of the model matrix, which may make the use of the exact test feasible even when $k$ is large.

One can also set exact="i" in which case the function simply returns the number of iterations required for an exact permutation test.

When using random permutations, the function ensures that the very first permutation will always correspond to the original data. This avoids p-values equal to 0.

Permutation-Based Confidence Intervals

When permci=TRUE, the function also tries to obtain permutation-based confidence intervals (CIs) of the model coefficient(s). This is done by shifting the observed effect sizes or outcomes by some amount and finding the most extreme values for this amount for which the permutation-based test would just lead to non-rejection. The calculation of such CIs is computationally expensive and may take a long time to complete. For models with moderators, one can also set permci to a vector of indices to specify for which coefficient(s) a permutation-based CI should be obtained. When the algorithm fails to determine a particular CI bound, it will be shown as NA in the output.

Permutation Tests for Location-Scale Models

The function also works with location-scale models (see rma.uni for details on such models). Permutation tests will then be carried out for both the location and scale parts of the model. However, note that permutation-based CIs are not available for location-scale models.

Value

An object of class "permutest.rma.uni". The object is a list containing the following components:

pval: p-value(s) based on the permutation test.
QMp: p-value for the omnibus test of moderators based on the permutation test.
zval.perm: values of the test statistics of the coefficients under the various permutations.
b.perm: the model coefficients under the various permutations.
QM.perm: the test statistic of the omnibus test of moderators under the various permutations.
ci.lb: lower bound of the confidence intervals for the coefficients (permutation-based when permci=TRUE).
ci.ub: upper bound of the confidence intervals for the coefficients (permutation-based when permci=TRUE).
...: some additional elements/values are passed on.

The results are formatted and printed with the print function. One can also use coef to obtain the table with the model coefficients, corresponding standard errors, test statistics, p-values, and confidence interval bounds. The permutation distribution(s) can be plotted with the plot function.

Note

The p-values obtained with permutation tests cannot reach conventional levels of statistical significance (i.e., $p \le .05$) when $k$ is very small. In particular, for models without moderators, the smallest possible (two-sided) p-value is .0625 when $k=5$ and .03125 when $k=6$. Therefore, the permutation test is only able to reject the null hypothesis at $\alpha=.05$ when $k$ is at least equal to 6. For models with moderators, the smallest possible (two-sided) p-value for a particular model coefficient is .0833 when $k=4$ and .0167 when $k=5$ (assuming that each row in the model matrix is unique). Therefore, the permutation test is only able to reject the null hypothesis at $\alpha=.05$ when $k$ is at least equal to 5. Consequently, permutation-based CIs can also only be obtained when $k$ is sufficiently large.

When the number of permutations required for the exact test is so large as to be essentially indistinguishable from infinity (e.g., factorial(200)), the function will terminate with an error.

Determining whether a test statistic under the permuted data is as extreme or more extreme than under the actually observed data requires making >= or <= comparisons. To avoid problems due to the finite precision with which computers generally represent numbers (see this FAQ for details), the function uses a numerical tolerance (control argument comptol, which is set equal to .Machine$double.eps^0.5 by default) when making such comparisons (e.g., instead of sqrt(3)^2 >= 3, which may evaluate to FALSE, we use sqrt(3)^2 >= 3 - .Machine$double.eps^0.5, which should evaluate to TRUE).

When obtaining permutation-based CIs, the function makes use of uniroot. By default, the desired accuracy is set equal to .Machine$double.eps^0.25 and the maximum number of iterations to 100. The desired accuracy and the maximum number of iterations can be adjusted with the control argument (i.e., control=list(tol=value, maxiter=value)). Also, the interval searched for the CI bounds may be too narrow, leading to NA for a bound. In this case, one can try setting control=list(distfac=value) with a value larger than 1 to extend the interval (the value indicating a multiplicative factor by which to extend the width of the interval searched) or control=list(extendInt="yes") to allow uniroot to extend the interval dynamically (in which case it can happen that a bound may try to drift to $\pm \infty$).

Author

Wolfgang Viechtbauer (wvb@metafor-project.org, https://www.metafor-project.org).

References

Follmann, D. A., & Proschan, M. A. (1999). Valid inference in random effects meta-analysis. Biometrics, 55(3), 732–737. https://doi.org/10.1111/j.0006-341x.1999.00732.x

Good, P. I. (2009). Permutation, parametric, and bootstrap tests of hypotheses (3rd ed.). New York: Springer.

Higgins, J. P. T., & Thompson, S. G. (2004). Controlling the risk of spurious findings from meta-regression. Statistics in Medicine, 23(11), 1663–1682. https://doi.org/10.1002/sim.1752

Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://doi.org/10.18637/jss.v036.i03

Viechtbauer, W., López-López, J. A., Sánchez-Meca, J., & Marín-Martínez, F. (2015). A comparison of procedures to test for moderators in mixed-effects meta-regression models. Psychological Methods, 20(3), 360–374. https://doi.org/10.1037/met0000023

Viechtbauer, W., & López-López, J. A. (2022). Location-scale models for meta-analysis. Research Synthesis Methods. 13(6), 697–715. https://doi.org/10.1002/jrsm.1562

Examples

### calculate log risk ratios and corresponding sampling variances
dat <- escalc(measure="RR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg)

### random-effects model
res <- rma(yi, vi, data=dat)
res
#> 
#> Random-Effects Model (k = 13; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of total heterogeneity): 0.3132 (SE = 0.1664)
#> tau (square root of estimated tau^2 value):      0.5597
#> I^2 (total heterogeneity / total variability):   92.22%
#> H^2 (total variability / sampling variability):  12.86
#> 
#> Test for Heterogeneity:
#> Q(df = 12) = 152.2330, p-val < .0001
#> 
#> Model Results:
#> 
#> estimate      se     zval    pval    ci.lb    ci.ub      
#>  -0.7145  0.1798  -3.9744  <.0001  -1.0669  -0.3622  *** 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 

### permutation test (approximate and exact)
set.seed(1234) # for reproducibility
permutest(res)
#> Running 1000 iterations for an approximate permutation test.
#> 
#> Model Results:
#> 
#> estimate      se     zval    pval¹    ci.lb    ci.ub     
#>  -0.7145  0.1798  -3.9744  0.0020   -1.0669  -0.3622  ** 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> 1) p-value based on permutation testing
#> 
permutest(res, exact=TRUE)
#> Running 8192 iterations for an exact permutation test.
#> 
#> Model Results:
#> 
#> estimate      se     zval    pval¹    ci.lb    ci.ub     
#>  -0.7145  0.1798  -3.9744  0.0015   -1.0669  -0.3622  ** 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> 1) p-value based on permutation testing
#> 

### mixed-effects model with two moderators (absolute latitude and publication year)
res <- rma(yi, vi, mods = ~ ablat + year, data=dat)
res
#> 
#> Mixed-Effects Model (k = 13; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of residual heterogeneity):     0.1108 (SE = 0.0845)
#> tau (square root of estimated tau^2 value):             0.3328
#> I^2 (residual heterogeneity / unaccounted variability): 71.98%
#> H^2 (unaccounted variability / sampling variability):   3.57
#> R^2 (amount of heterogeneity accounted for):            64.63%
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 10) = 28.3251, p-val = 0.0016
#> 
#> Test of Moderators (coefficients 2:3):
#> QM(df = 2) = 12.2043, p-val = 0.0022
#> 
#> Model Results:
#> 
#>          estimate       se     zval    pval     ci.lb    ci.ub     
#> intrcpt   -3.5455  29.0959  -0.1219  0.9030  -60.5724  53.4814     
#> ablat     -0.0280   0.0102  -2.7371  0.0062   -0.0481  -0.0080  ** 
#> year       0.0019   0.0147   0.1299  0.8966   -0.0269   0.0307     
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 

### number of iterations required for an exact permutation test
permutest(res, exact="i")
#> [1] 6227020800

### permutation test (approximate only; exact not feasible)
set.seed(1234) # for reproducibility
permres <- permutest(res, iter=10000)
#> Running 10000 iterations for an approximate permutation test.
permres
#> 
#> Test of Moderators (coefficients 2:3):¹
#> QM(df = 2) = 12.2043, p-val = 0.0237
#> 
#> Model Results:
#> 
#>          estimate       se     zval    pval¹     ci.lb    ci.ub    
#> intrcpt   -3.5455  29.0959  -0.1219  0.9104   -60.5724  53.4814    
#> ablat     -0.0280   0.0102  -2.7371  0.0175    -0.0481  -0.0080  * 
#> year       0.0019   0.0147   0.1299  0.9037    -0.0269   0.0307    
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> 1) p-values based on permutation testing
#> 

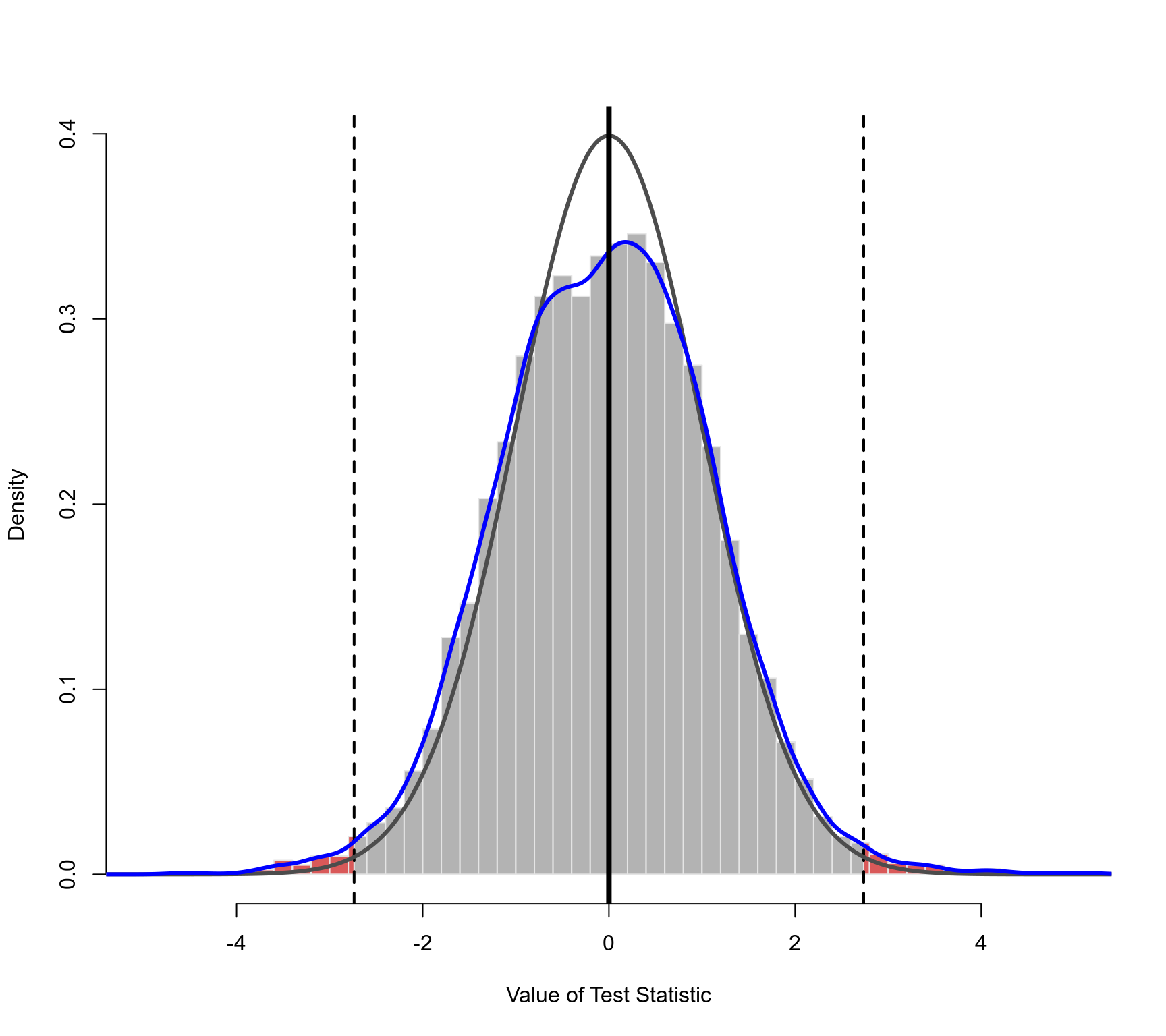
### plot of the permutation distribution for absolute latitude
### dashed horizontal line: the observed value of the test statistic (in both tails)
### black curve: standard normal density (theoretical reference/null distribution)
### blue curve: kernel density estimate of the permutation distribution
### note: the tail area under the permutation distribution is larger
### than under a standard normal density (hence, the larger p-value)
plot(permres, beta=2, lwd=c(2,3,3,4), xlim=c(-5,5))


### mixed-effects model with a categorical and a quantitative moderator
res <- rma(yi, vi, mods = ~ ablat + alloc, data=dat)
res
#> 
#> Mixed-Effects Model (k = 13; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of residual heterogeneity):     0.1446 (SE = 0.1124)
#> tau (square root of estimated tau^2 value):             0.3803
#> I^2 (residual heterogeneity / unaccounted variability): 70.11%
#> H^2 (unaccounted variability / sampling variability):   3.35
#> R^2 (amount of heterogeneity accounted for):            53.84%
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 9) = 26.2034, p-val = 0.0019
#> 
#> Test of Moderators (coefficients 2:4):
#> QM(df = 3) = 11.0605, p-val = 0.0114
#> 
#> Model Results:
#> 
#>                  estimate      se     zval    pval    ci.lb    ci.ub     
#> intrcpt            0.2932  0.4050   0.7239  0.4691  -0.5006   1.0870     
#> ablat             -0.0273  0.0092  -2.9650  0.0030  -0.0453  -0.0092  ** 
#> allocrandom       -0.2675  0.3504  -0.7633  0.4453  -0.9543   0.4193     
#> allocsystematic    0.0585  0.3795   0.1540  0.8776  -0.6854   0.8023     
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 

### permutation test testing the allocation factor coefficients
set.seed(1234) # for reproducibility
permutest(res, btt="alloc")
#> Running 1000 iterations for an approximate permutation test.
#> 
#> Test of Moderators (coefficients 3:4):¹
#> QM(df = 2) = 1.2850, p-val = 0.5530
#> 
#> Model Results:
#> 
#>                  estimate      se     zval    pval¹    ci.lb    ci.ub    
#> intrcpt            0.2932  0.4050   0.7239  0.6710   -0.5006   1.0870    
#> ablat             -0.0273  0.0092  -2.9650  0.0230   -0.0453  -0.0092  * 
#> allocrandom       -0.2675  0.3504  -0.7633  0.4700   -0.9543   0.4193    
#> allocsystematic    0.0585  0.3795   0.1540  0.8700   -0.6854   0.8023    
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> 1) p-values based on permutation testing
#>