Model Diagnostics for 'rma.mv' Objects
influence.rma.mv.RdFunctions to compute various outlier and influential study diagnostics (some of which indicate the influence of deleting one study at a time on the model fit or the fitted/residual values) for objects of class "rma.mv".
# S3 method for class 'rma.mv'
cooks.distance(model, progbar=FALSE, cluster,
reestimate=TRUE, parallel="no", ncpus=1, cl, ...)
# S3 method for class 'rma.mv'
dfbetas(model, progbar=FALSE, cluster,
reestimate=TRUE, parallel="no", ncpus=1, cl, ...)
# S3 method for class 'rma.mv'
hatvalues(model, type="diagonal", ...)Arguments
- model
an object of class
"rma.mv".- progbar
logical to specify whether a progress bar should be shown (the default is
FALSE).- cluster
optional vector to specify a clustering variable to use for computing the Cook's distances or DFBETAS values. If unspecified, these measures are computed for the individual observed effect sizes or outcomes.
- reestimate
logical to specify whether variance/correlation components should be re-estimated after deletion of the \(i\text{th}\) case (the default is
TRUE).- parallel
character string to specify whether parallel processing should be used (the default is
"no"). For parallel processing, set to either"snow"or"multicore". See ‘Note’.- ncpus
integer to specify the number of processes to use in the parallel processing.
- cl
optional cluster to use if
parallel="snow". If unspecified, a cluster on the local machine is created for the duration of the call.- type
character string to specify whether only the diagonal of the hat matrix (
"diagonal") or the entire hat matrix ("matrix") should be returned.- ...
other arguments.
Details
The term ‘case’ below refers to a particular row from the dataset used in the model fitting (when argument cluster is not specified) or each level of the variable specified via cluster.
Cook's distance for the \(i\text{th}\) case can be interpreted as the Mahalanobis distance between the entire set of predicted values once with the \(i\text{th}\) case included and once with the \(i\text{th}\) case excluded from the model fitting.
The DFBETAS value(s) essentially indicate(s) how many standard deviations the estimated coefficient(s) change(s) after excluding the \(i\text{th}\) case from the model fitting.
Value
The cooks.distance function returns a vector. The dfbetas function returns a data frame. The hatvalues function returns either a vector with the diagonal elements of the hat matrix or the entire hat matrix.
Note
The variable specified via cluster is assumed to be of the same length as the data originally passed to the rma.mv function (and if the data argument was used in the original model fit, then the variable will be searched for within this data frame first). Any subsetting and removal of studies with missing values that was applied during the model fitting is also automatically applied to the variable specified via the cluster argument.
Leave-one-out diagnostics are calculated by refitting the model \(k\) times (where \(k\) denotes the number of cases). Depending on how large \(k\) is, it may take a few moments to finish the calculations. For complex models fitted with rma.mv, this can become computationally expensive.
On machines with multiple cores, one can try to speed things up by delegating the model fitting to separate worker processes, that is, by setting parallel="snow" or parallel="multicore" and ncpus to some value larger than 1. Parallel processing makes use of the parallel package, using the makePSOCKcluster and parLapply functions when parallel="snow" or using mclapply when parallel="multicore" (the latter only works on Unix/Linux-alikes). With parallel::detectCores(), one can check on the number of available cores on the local machine.
Alternatively (or in addition to using parallel processing), one can also set reestimate=FALSE, in which case any variance/correlation components in the model are not re-estimated after deleting the \(i\text{th}\) case from the dataset. Doing so only yields an approximation to the Cook's distances and DFBETAS values that ignores the influence of the \(i\text{th}\) case on the variance/correlation components, but is considerably faster (and often yields similar results).
It may not be possible to fit the model after deletion of the \(i\text{th}\) case from the dataset. This will result in NA values for that case.
References
Belsley, D. A., Kuh, E., & Welsch, R. E. (1980). Regression diagnostics. New York: Wiley.
Cook, R. D., & Weisberg, S. (1982). Residuals and influence in regression. London: Chapman and Hall.
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://doi.org/10.18637/jss.v036.i03
Viechtbauer, W. (2021). Model checking in meta-analysis. In C. H. Schmid, T. Stijnen, & I. R. White (Eds.), Handbook of meta-analysis (pp. 219–254). Boca Raton, FL: CRC Press. https://doi.org/10.1201/9781315119403
Viechtbauer, W., & Cheung, M. W.-L. (2010). Outlier and influence diagnostics for meta-analysis. Research Synthesis Methods, 1(2), 112–125. https://doi.org/10.1002/jrsm.11
Examples
### copy data from Konstantopoulos (2011) into 'dat'
dat <- dat.konstantopoulos2011
### multilevel random-effects model
res <- rma.mv(yi, vi, random = ~ 1 | district/school, data=dat)
print(res, digits=3)
#>
#> Multivariate Meta-Analysis Model (k = 56; method: REML)
#>
#> Variance Components:
#>
#> estim sqrt nlvls fixed factor
#> sigma^2.1 0.065 0.255 11 no district
#> sigma^2.2 0.033 0.181 56 no district/school
#>
#> Test for Heterogeneity:
#> Q(df = 55) = 578.864, p-val < .001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> 0.185 0.085 2.185 0.029 0.019 0.350 *
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
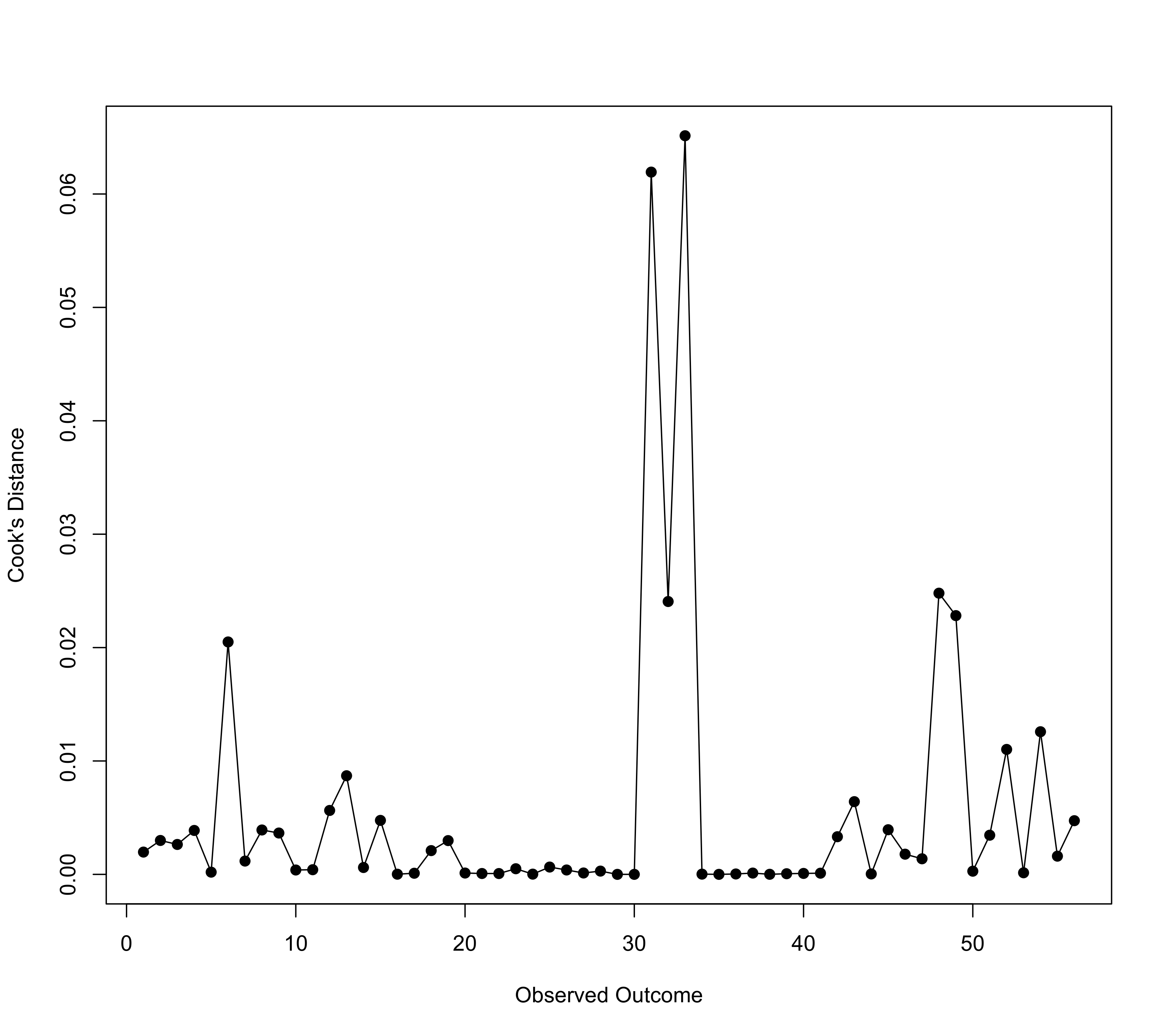
### Cook's distance for each observed outcome
x <- cooks.distance(res)
x
#> 1 2 3 4 5 6 7
#> 1.965212e-03 2.989769e-03 2.638140e-03 3.873368e-03 1.954562e-04 2.049672e-02 1.172821e-03
#> 8 9 10 11 12 13 14
#> 3.913806e-03 3.646294e-03 3.850068e-04 4.111673e-04 5.636933e-03 8.697462e-03 6.052503e-04
#> 15 16 17 18 19 20 21
#> 4.759729e-03 1.527261e-05 9.905788e-05 2.095987e-03 2.978160e-03 1.173555e-04 7.600104e-05
#> 22 23 24 25 26 27 28
#> 7.315289e-05 4.966021e-04 2.024080e-05 6.448093e-04 3.866063e-04 1.220054e-04 2.886483e-04
#> 29 30 31 32 33 34 35
#> 7.676475e-08 1.391702e-06 6.193156e-02 2.406239e-02 6.513879e-02 2.075376e-05 8.763824e-07
#> 36 37 38 39 40 41 42
#> 3.485720e-05 1.141739e-04 6.503505e-06 5.671804e-05 8.326350e-05 1.048009e-04 3.320742e-03
#> 43 44 45 46 47 48 49
#> 6.412251e-03 3.831098e-05 3.937144e-03 1.780433e-03 1.374408e-03 2.479767e-02 2.281846e-02
#> 50 51 52 53 54 55 56
#> 2.803636e-04 3.453698e-03 1.101867e-02 1.405348e-04 1.257869e-02 1.606173e-03 4.733738e-03
plot(x, type="o", pch=19, xlab="Observed Outcome", ylab="Cook's Distance")
### Cook's distance for each district
x <- cooks.distance(res, cluster=district)
x
#> 11 12 18 27 56 58 71
#> 0.0693784141 0.0161880605 0.0419849758 0.1192089451 0.0213566370 0.1014506985 0.5585174855
#> 86 91 108 644
#> 0.0656500673 0.0037438517 0.0548839761 0.0003441647
plot(x, type="o", pch=19, xlab="District", ylab="Cook's Distance", xaxt="n")
axis(side=1, at=seq_along(x), labels=as.numeric(names(x)))
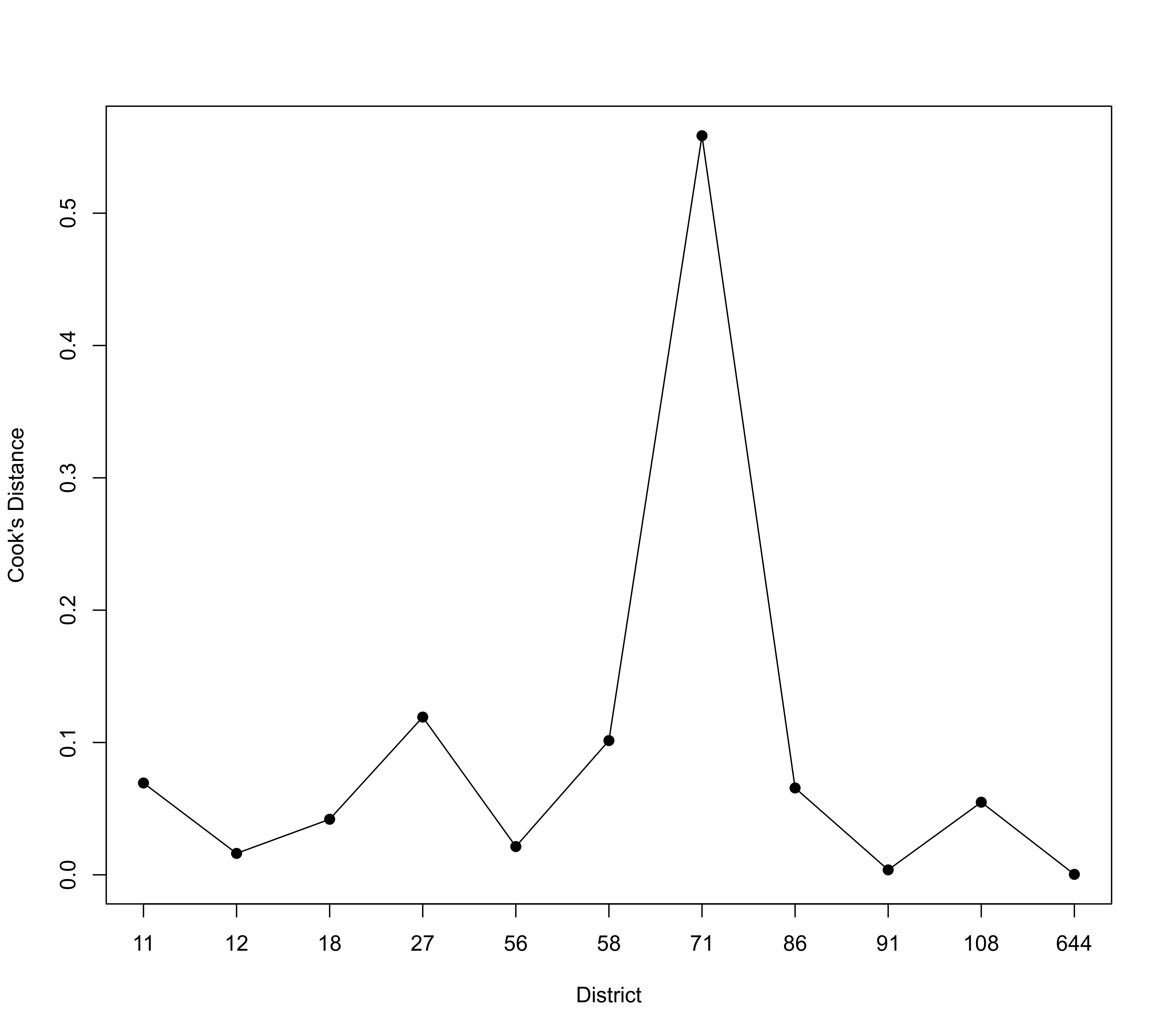### hat values
hatvalues(res)
#> 1 2 3 4 5 6 7 8
#> 0.018246414 0.018246414 0.015562154 0.015562154 0.024305990 0.024305990 0.023796820 0.020021978
#> 9 10 11 12 13 14 15 16
#> 0.028628711 0.021068630 0.035668057 0.018288352 0.026253550 0.026253550 0.024271478 0.018700077
#> 17 18 19 20 21 22 23 24
#> 0.024347299 0.025637683 0.026335563 0.008149594 0.008470846 0.008307115 0.007851819 0.008149594
#> 25 26 27 28 29 30 31 32
#> 0.007997936 0.011094988 0.010815774 0.010815774 0.010815774 0.010815774 0.027875751 0.030425177
#> 33 34 35 36 37 38 39 40
#> 0.031137102 0.012900198 0.012900198 0.012900198 0.012900198 0.012900198 0.012900198 0.012900198
#> 41 42 43 44 45 46 47 48
#> 0.012900198 0.016836925 0.016451963 0.016836925 0.017240335 0.015732539 0.015732539 0.018231717
#> 49 50 51 52 53 54 55 56
#> 0.018231717 0.018522325 0.018522325 0.018522325 0.017484652 0.018246600 0.020990821 0.020990821