Forest Plots (Default Method)
forest.default.RdFunction to create forest plots for a given set of data.
# Default S3 method
forest(x, vi, sei, ci.lb, ci.ub,
annotate=TRUE, showweights=FALSE, header=TRUE,
xlim, alim, olim, ylim, at, steps=5,
level=95, refline=0, digits=2L, width,
xlab, slab, ilab, ilab.lab, ilab.xpos, ilab.pos,
order, subset, transf, atransf, targs, rows,
efac=1, pch, psize, plim=c(0.5,1.5), col,
shade, colshade, lty, fonts, cex, cex.lab, cex.axis, ...)Arguments
- x
vector of length \(k\) with the observed effect sizes or outcomes.
- vi
vector of length \(k\) with the corresponding sampling variances.
- sei
vector of length \(k\) with the corresponding standard errors (note: only one of the two,
viorsei, needs to be specified).- ci.lb
vector of length \(k\) with the corresponding lower confidence interval bounds. Not needed if
viorseiis specified. See ‘Details’.- ci.ub
vector of length \(k\) with the corresponding upper confidence interval bounds. Not needed if
viorseiis specified. See ‘Details’.- annotate
logical to specify whether annotations should be added to the plot (the default is
TRUE).- showweights
logical to specify whether the annotations should also include the inverse variance weights (the default is
FALSE).- header
logical to specify whether column headings should be added to the plot (the default is
TRUE). Can also be a character vector to specify the left and right headings (or only the left one).- xlim
horizontal limits of the plot region. If unspecified, the function sets the horizontal plot limits to some sensible values.
- alim
the x-axis limits. If unspecified, the function sets the x-axis limits to some sensible values.
- olim
argument to specify observation/outcome limits. If unspecified, no limits are used.
- ylim
the y-axis limits of the plot. If unspecified, the function sets the y-axis limits to some sensible values. Can also be a single value to set the lower bound (while the upper bound is still set automatically).
- at
position of the x-axis tick marks and corresponding labels. If unspecified, the function sets the tick mark positions/labels to some sensible values.
- steps
the number of tick marks for the x-axis (the default is 5). Ignored when the positions are specified via the
atargument.- level
numeric value between 0 and 100 to specify the confidence interval level (the default is 95; see here for details).
- refline
numeric value to specify the location of the vertical ‘reference’ line (the default is 0). The line can be suppressed by setting this argument to
NA. Can also be a vector to add multiple lines.- digits
integer to specify the number of decimal places to which the annotations and tick mark labels of the x-axis should be rounded (the default is
2L). Can also be a vector of two integers, the first to specify the number of decimal places for the annotations, the second for the x-axis labels (whenshowweights=TRUE, can also specify a third value for the weights). When specifying an integer (e.g.,2L), trailing zeros after the decimal mark are dropped for the x-axis labels. When specifying a numeric value (e.g.,2), trailing zeros are retained.- width
optional integer to manually adjust the width of the columns for the annotations (either a single integer or a vector of the same length as the number of annotation columns).
- xlab
title for the x-axis. If unspecified, the function sets an appropriate axis title. Can also be a vector of three/two values (to also/only add labels at the end points of the x-axis limits).
- slab
optional vector with labels for the \(k\) studies. If unspecified, the function tries to extract study labels from
xand otherwise simple labels are created within the function. To suppress labels, set this argument toNA.- ilab
optional vector, matrix, or data frame providing additional information about the studies that should be added to the plot.
- ilab.lab
optional character vector with (column) labels for the variable(s) given via
ilab.- ilab.xpos
optional numeric vector to specify the horizontal position(s) of the variable(s) given via
ilab.- ilab.pos
integer(s) (either 1, 2, 3, or 4) to specify the alignment of the variable(s) given via
ilab(2 means right, 4 means left aligned). If unspecified, the default is to center the values.- order
optional character string to specify how the studies should be ordered. Can also be a variable based on which the studies will be ordered. See ‘Details’.
- subset
optional (logical or numeric) vector to specify the subset of studies that should be included in the plot.
- transf
optional argument to specify a function to transform the observed outcomes and corresponding confidence interval bounds (e.g.,
transf=exp; see also transf). If unspecified, no transformation is used.- atransf
optional argument to specify a function to transform the x-axis labels and annotations (e.g.,
atransf=exp; see also transf). If unspecified, no transformation is used.- targs
optional arguments needed by the function specified via
transforatransf.- rows
optional vector to specify the rows (or more generally, the positions) for plotting the outcomes. Can also be a single value to specify the row of the first outcome (the remaining outcomes are then plotted below this starting row).
- efac
vertical expansion factor for confidence interval limits and arrows. The default value of 1 should usually work fine. Can also be a vector of two numbers, the first for CI limits, the second for arrows.
- pch
plotting symbol to use for the observed outcomes. By default, a filled square is used. See
pointsfor other options. Can also be a vector of values.- psize
optional numeric value to specify the point sizes for the observed outcomes. If unspecified, the point sizes are a function of the precision of the estimates. Can also be a vector of values.
- plim
numeric vector of length 2 to scale the point sizes (ignored when
psizeis specified). See ‘Details’.- col
optional character string to specify the color of the observed outcomes. Can also be a vector.
- shade
optional character string or a (logical or numeric) vector for shading rows of the plot. See ‘Details’.
- colshade
optional argument to specify the color for the shading.
- lty
optional argument to specify the line type for the confidence intervals. If unspecified, the function sets this to
"solid"by default.- fonts
optional character string to specify the font for the study labels, annotations, and the extra information (if specified via
ilab). If unspecified, the default font is used.- cex
optional character and symbol expansion factor. If unspecified, the function sets this to a sensible value.
- cex.lab
optional expansion factor for the x-axis title. If unspecified, the function sets this to a sensible value.
- cex.axis
optional expansion factor for the x-axis labels. If unspecified, the function sets this to a sensible value.
- ...
other arguments.
Details
The plot shows the observed effect sizes or outcomes (by default as filled squares) with corresponding level% confidence intervals (as horizontal lines extending from the observed outcomes). To use the function, one should specify the observed outcomes (via the x argument) together with the corresponding sampling variances (via the vi argument) or with the corresponding standard errors (via the sei argument). The confidence intervals are computed with \(y_i \pm z_{crit} \sqrt{v_i}\), where \(y_i\) denotes the observed outcome in the \(i\text{th}\) study, \(v_i\) the corresponding sampling variance (and hence \(\sqrt{v_i}\) is the corresponding standard error), and \(z_{crit}\) is the appropriate critical value from a standard normal distribution (e.g., \(1.96\) for a 95% CI). Alternatively, one can directly specify the confidence interval bounds via the ci.lb and ci.ub arguments.
Applying a Transformation
With the transf argument, the observed outcomes and corresponding confidence interval bounds can be transformed with some suitable function. For example, when plotting log odds ratios, then one could use transf=exp to obtain a forest plot showing the odds ratios. Alternatively, one can use the atransf argument to transform the x-axis labels and annotations (e.g., atransf=exp). See also transf for some other useful transformation functions in the context of a meta-analysis. The examples below illustrate the use of these arguments.
Ordering of Studies
By default, the studies are ordered from top to bottom (i.e., the first study in the dataset will be placed in row \(k\), the second study in row \(k-1\), and so on, until the last study, which is placed in the first row). The studies can be reordered with the order argument:
order="obs": the studies are ordered by the observed outcomes,order="prec": the studies are ordered by their sampling variances.
Alternatively, it is also possible to set order equal to a variable based on which the studies will be ordered (see ‘Examples’). One can also use the rows argument to specify the rows (or more generally, the positions) for plotting the outcomes.
Adding Additional Information to the Plot
Additional columns with information about the studies can be added to the plot via the ilab argument. This can either be a single variable or an entire matrix / data frame (with as many rows as there are studies in the forest plot). The ilab.xpos argument can be used to specify the horizontal position of the variables specified via ilab. The ilab.pos argument can be used to specify how the variables should be aligned. The ilab.lab argument can be used to add headers to the columns.
Pooled estimates can be added to the plot as polygons with the addpoly function. See the documentation for that function for examples.
Adjusting the Point Sizes
By default (i.e., when psize is not specified), the point sizes are a function of the precision (i.e., inverse standard errors) of the outcomes. This way, more precise estimates are visually more prominent in the plot. By making the point sizes a function of the inverse standard errors of the estimates, their areas are proportional to the inverse sampling variances, which corresponds to the weights they would receive in an equal-effects model. However, the point sizes are rescaled so that the smallest point size is plim[1] and the largest point size is plim[2]. As a result, their relative sizes (i.e., areas) no longer exactly correspond to their relative weights in such a model. If exactly relative point sizes are desired, one can set plim[2] to NA, in which case the points are rescaled so that the smallest point size corresponds to plim[1] and all other points are scaled accordingly. As a result, the largest point may be very large. Alternatively, one can set plim[1] to NA, in which case the points are rescaled so that the largest point size corresponds to plim[2] and all other points are scaled accordingly. As a result, the smallest point may be very small and essentially indistinguishable from the confidence interval line. To avoid the latter, one can also set plim[3], which enforces a minimal point size.
Shading Rows
With the shade argument, one can shade rows of the plot. The argument can be set to one of the following character strings: "zebra" (same as shade=TRUE) or "zebra2" to use zebra-style shading (starting either at the first or second study) or to "all" in which case all rows are shaded. Alternatively, the argument can be set to a logical or numeric vector to specify which rows should be shaded. The colshade argument can be used to set the color of shaded rows.
Note
The function sets some sensible values for the optional arguments, but it may be necessary to adjust these in certain circumstances.
The function actually returns some information about the chosen values invisibly. Printing this information is useful as a starting point to customize the plot.
If the number of studies is quite large, the labels, annotations, and symbols may become quite small and impossible to read. Stretching the plot window vertically may then provide a more readable figure (one should call the function again after adjusting the window size, so that the label/symbol sizes can be properly adjusted). Also, the cex, cex.lab, and cex.axis arguments are then useful to adjust the symbol and text sizes.
If the outcome measure used for creating the plot is bounded (e.g., correlations are bounded between -1 and +1, proportions are bounded between 0 and 1), one can use the olim argument to enforce those limits (the observed outcomes and confidence intervals cannot exceed those bounds then).
The lty argument can also be a vector of two elements, the first for specifying the line type of the individual CIs ("solid" by default), the second for the line type of the horizontal line that is automatically added to the plot ("solid" by default; set to "blank" to remove it).
Additional Optional Arguments
There are some additional optional arguments that can be passed to the function via ... (hence, they cannot be abbreviated):
- top
single numeric value to specify the amount of space (in terms of number of rows) to leave empty at the top of the plot (e.g., for adding headers). The default is 3.
- annosym
vector of length 3 to select the left bracket, separation, and right bracket symbols for the annotations. The default is
c(" [", ", ", "]"). Can also include a 4th element to adjust the look of the minus symbol, for example to use a proper minus sign (−) instead of a hyphen-minus (-). Can also include a 5th element that should be a space-like symbol (e.g., an ‘en space’) that is used in place of numbers (only relevant when trying to line up numbers exactly). For example,annosym=c(" [", ", ", "]", "\u2212", "\u2002")would use a proper minus sign and an ‘en space’ for the annotations. The decimal point character can be adjusted via theOutDecargument of theoptionsfunction before creating the plot (e.g.,options(OutDec=",")).- tabfig
single numeric value (either a 1, 2, or 3) to set
annosymautomatically to a vector that will exactly align the numbers in the annotations when using a font that provides ‘tabular figures’. Value 1 corresponds to using"\u2212"(a minus) and"\u2002"(an ‘en space’) inannoyymas shown above. Value 2 corresponds to"\u2013"(an ‘en dash’) and"\u2002"(an ‘en space’). Value 3 corresponds to"\u2212"(a minus) and"\u2007"(a ‘figure space’). The appropriate value for this argument depends on the font used. For example, for fonts Calibri and Carlito, 1 or 2 should work; for fonts Source Sans 3 and Palatino Linotype, 1, 2, and 3 should all work; for Computer/Latin Modern and Segoe UI, 2 should work; for Lato, Roboto, and Open Sans (and maybe Arial), 3 should work. Other fonts may work as well, but this is untested.- textpos
numeric vector of length 2 to specify the placement of the study labels and the annotations. The default is to use the horizontal limits of the plot region, i.e., the study labels to the right of
xlim[1]and the annotations to the left ofxlim[2].- rowadj
numeric vector of length 3 to vertically adjust the position of the study labels, the annotations, and the extra information (if specified via
ilab). This is useful for fine-tuning the position of text added with different positional alignments (i.e., argumentposin thetextfunction).
References
Lewis, S., & Clarke, M. (2001). Forest plots: Trying to see the wood and the trees. British Medical Journal, 322(7300), 1479–1480. https://doi.org/10.1136/bmj.322.7300.1479
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://doi.org/10.18637/jss.v036.i03
See also
forest for an overview of the various forest functions and especially forest.rma for a function to draw forest plots including a pooled estimate polygon.
addpoly for a function to add polygons to forest plots.
Examples
### calculate log risk ratios and corresponding sampling variances
dat <- escalc(measure="RR", ai=tpos, bi=tneg, ci=cpos, di=cneg,
data=dat.bcg, slab=paste(author, year, sep=", "))
### default forest plot of the observed log risk ratios
forest(dat$yi, dat$vi)
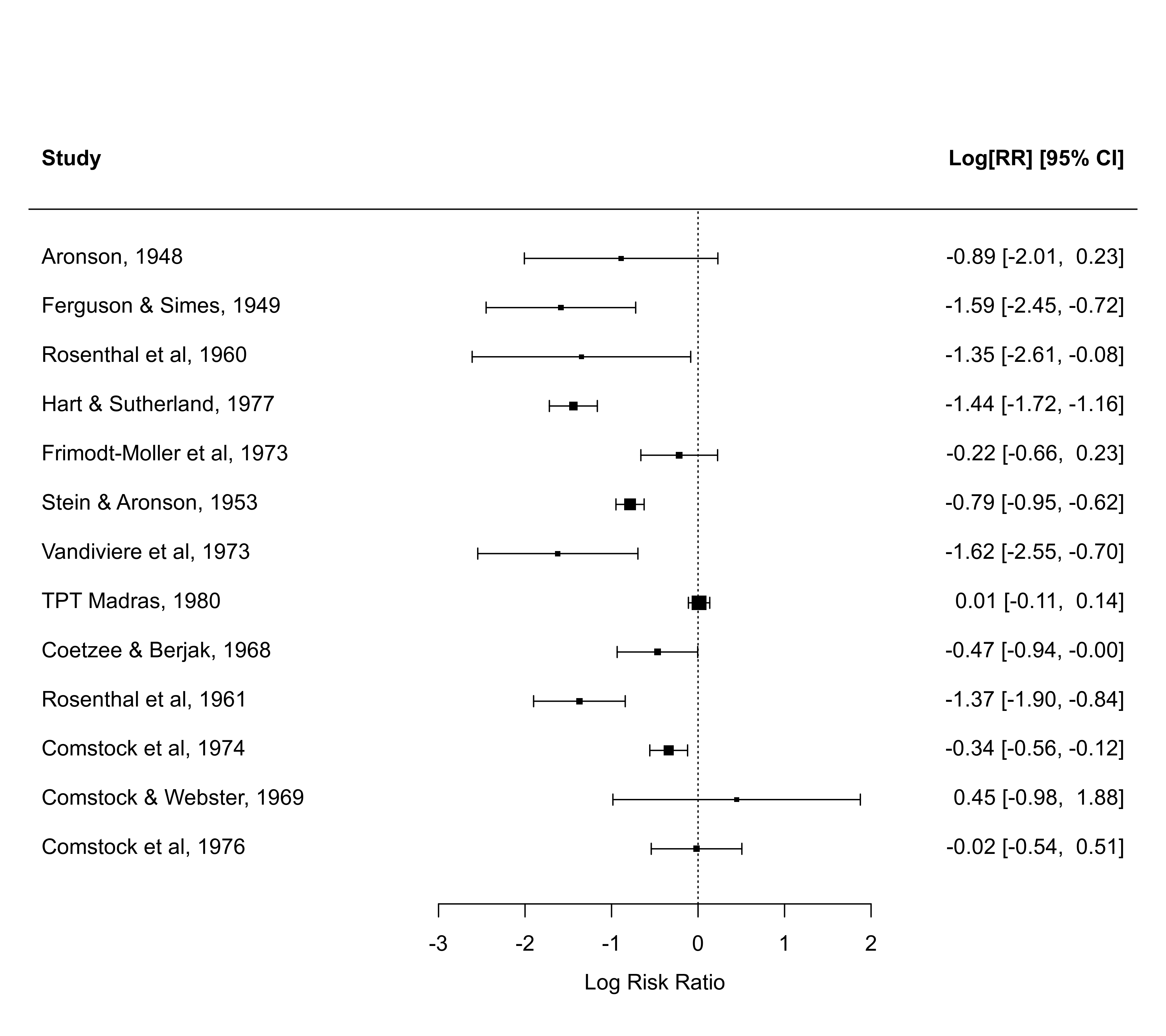 ### directly specify the CI bounds
out <- summary(dat)
forest(dat$yi, ci.lb=out$ci.lb, ci.ub=out$ci.ub)
### directly specify the CI bounds
out <- summary(dat)
forest(dat$yi, ci.lb=out$ci.lb, ci.ub=out$ci.ub)
 ### the with() function can be used to avoid having to retype dat$... over and over
with(dat, forest(yi, vi))
### the with() function can be used to avoid having to retype dat$... over and over
with(dat, forest(yi, vi))
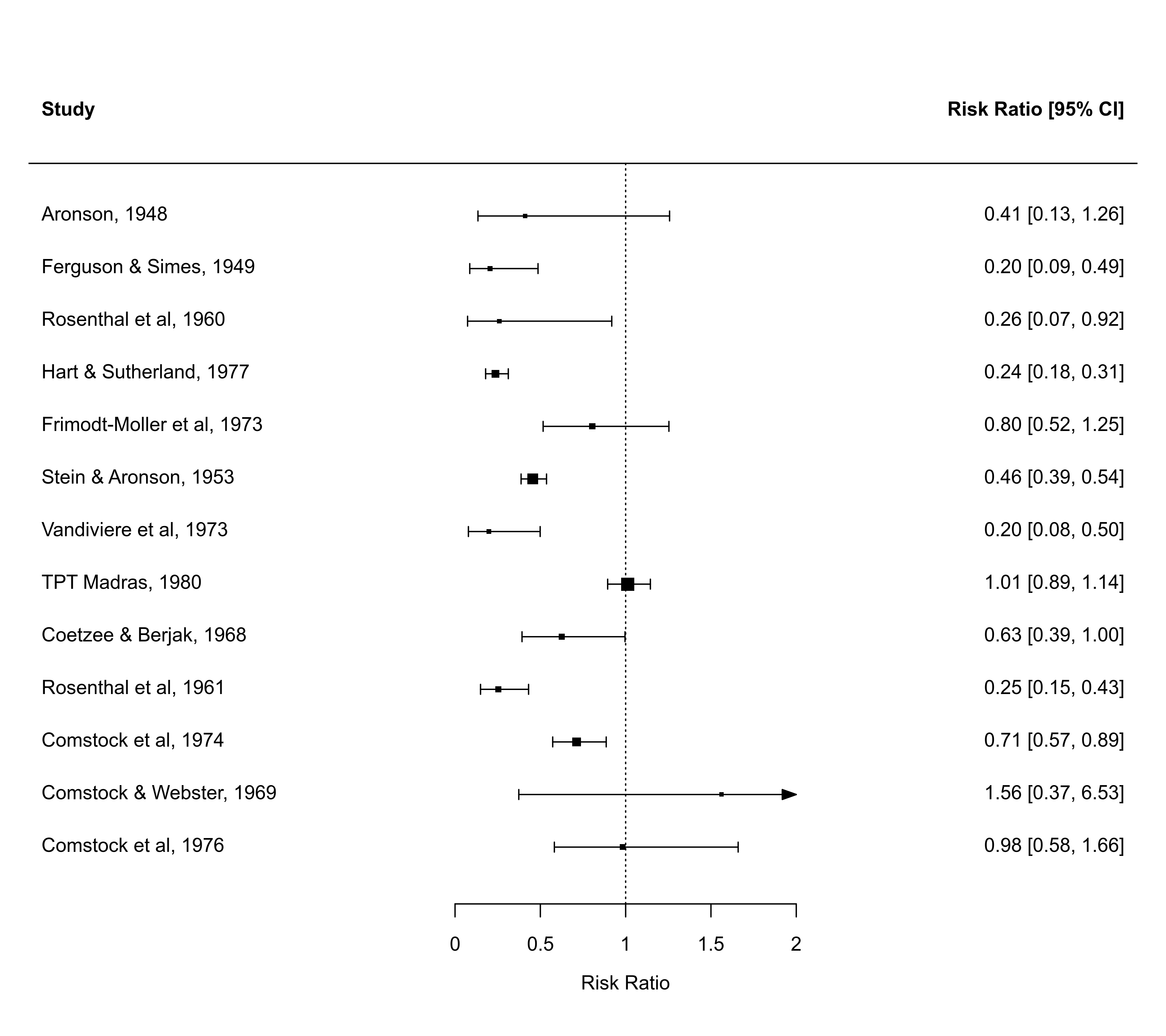
 ### forest plot of the observed risk ratios (transform outcomes)
with(dat, forest(yi, vi, transf=exp, alim=c(0,2), steps=5,
xlim=c(-2.5,4), refline=1))
### forest plot of the observed risk ratios (transform outcomes)
with(dat, forest(yi, vi, transf=exp, alim=c(0,2), steps=5,
xlim=c(-2.5,4), refline=1))
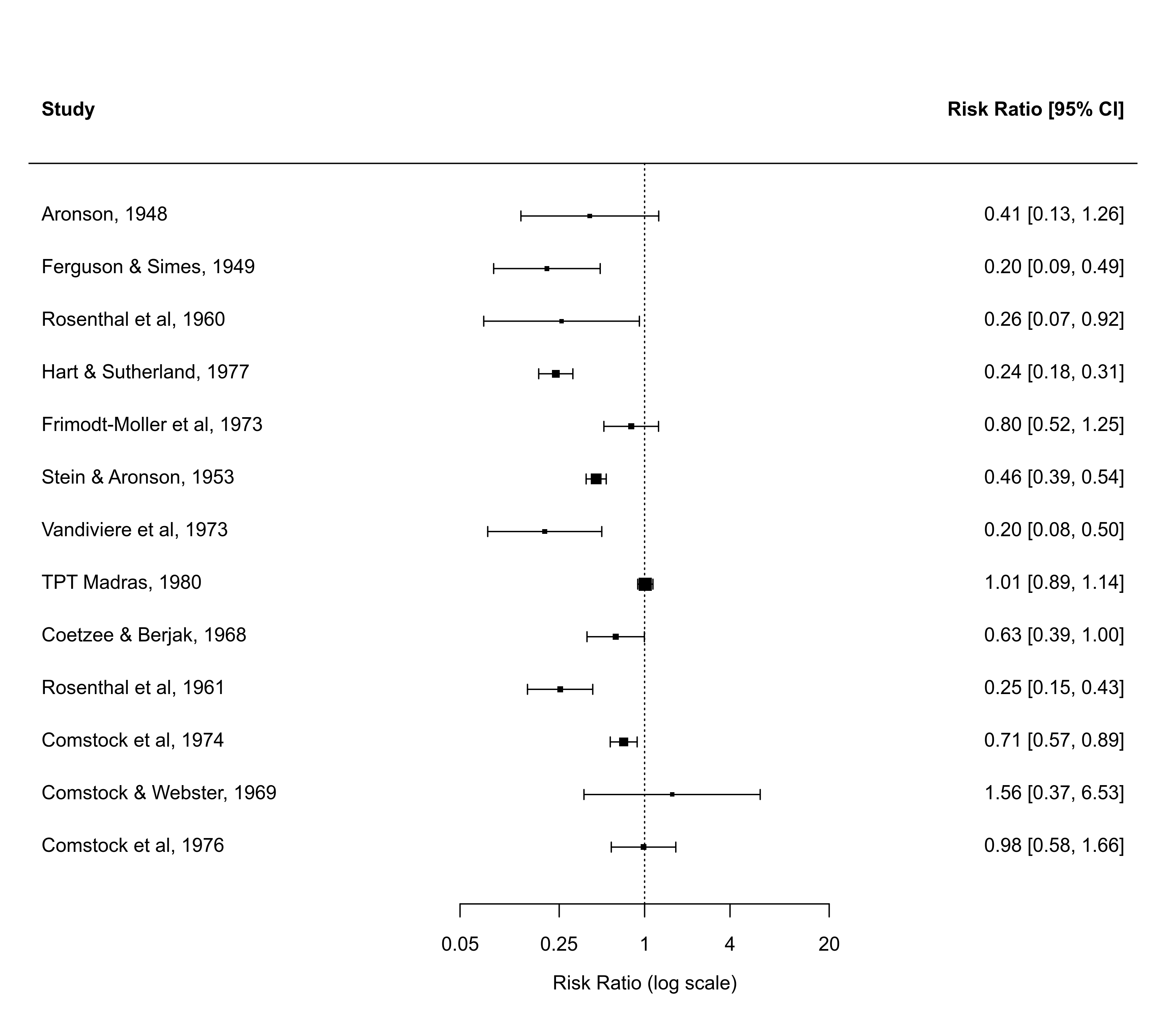
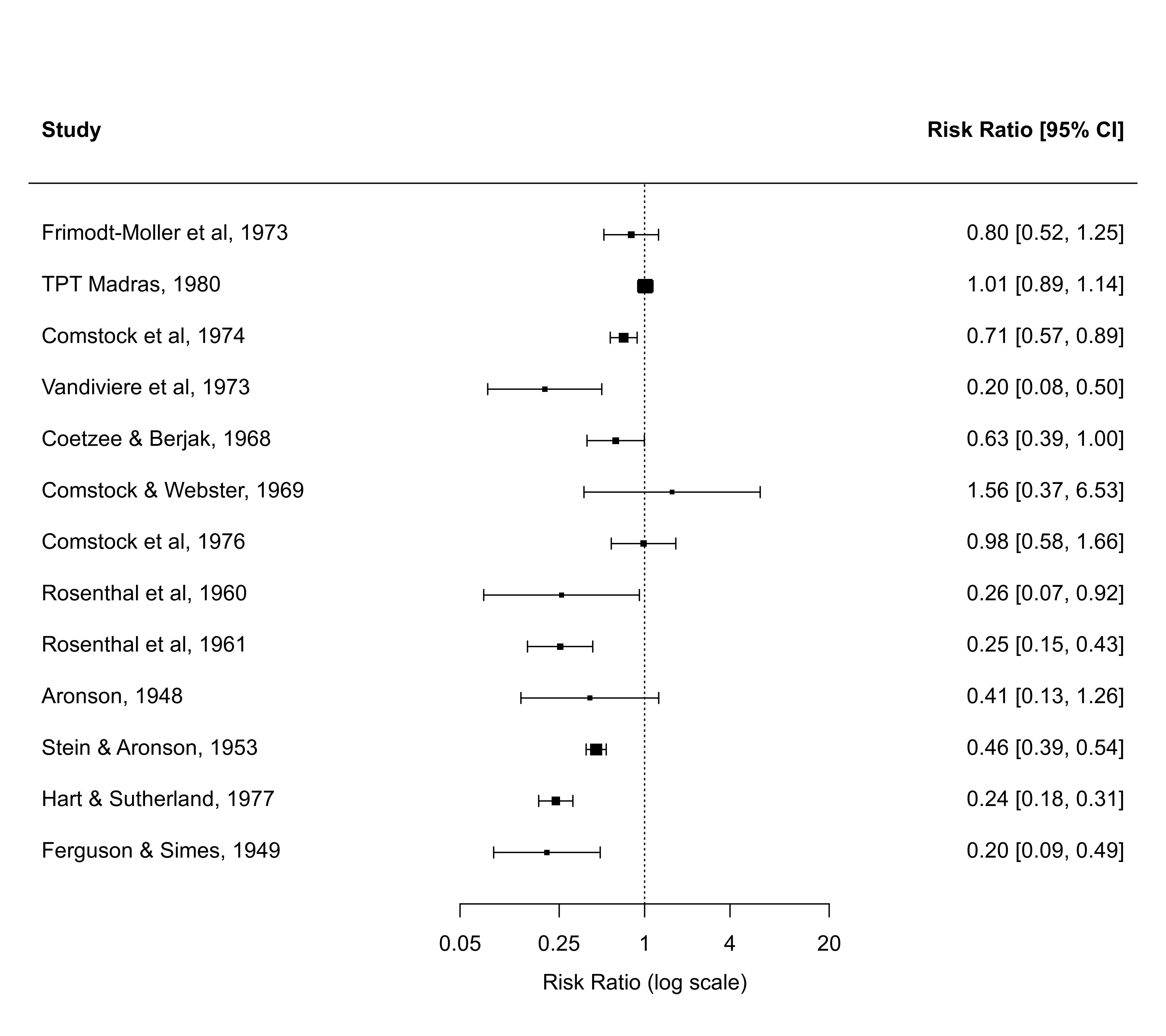
 ### forest plot of the observed risk ratios (transformed x-axis)
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8)))
### forest plot of the observed risk ratios (transformed x-axis)
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8)))
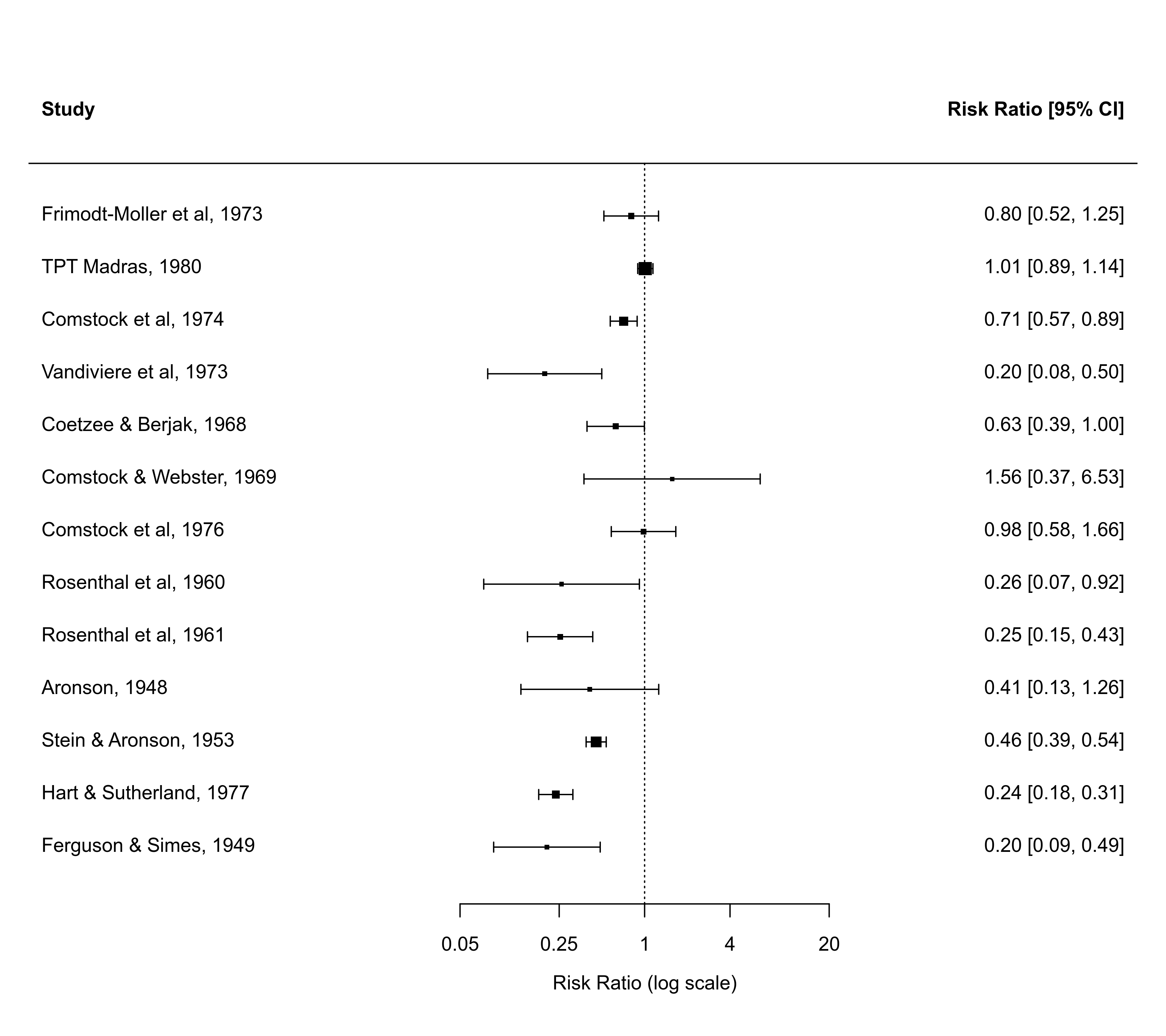 ### make all points the same size
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8), psize=1))
### make all points the same size
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8), psize=1))
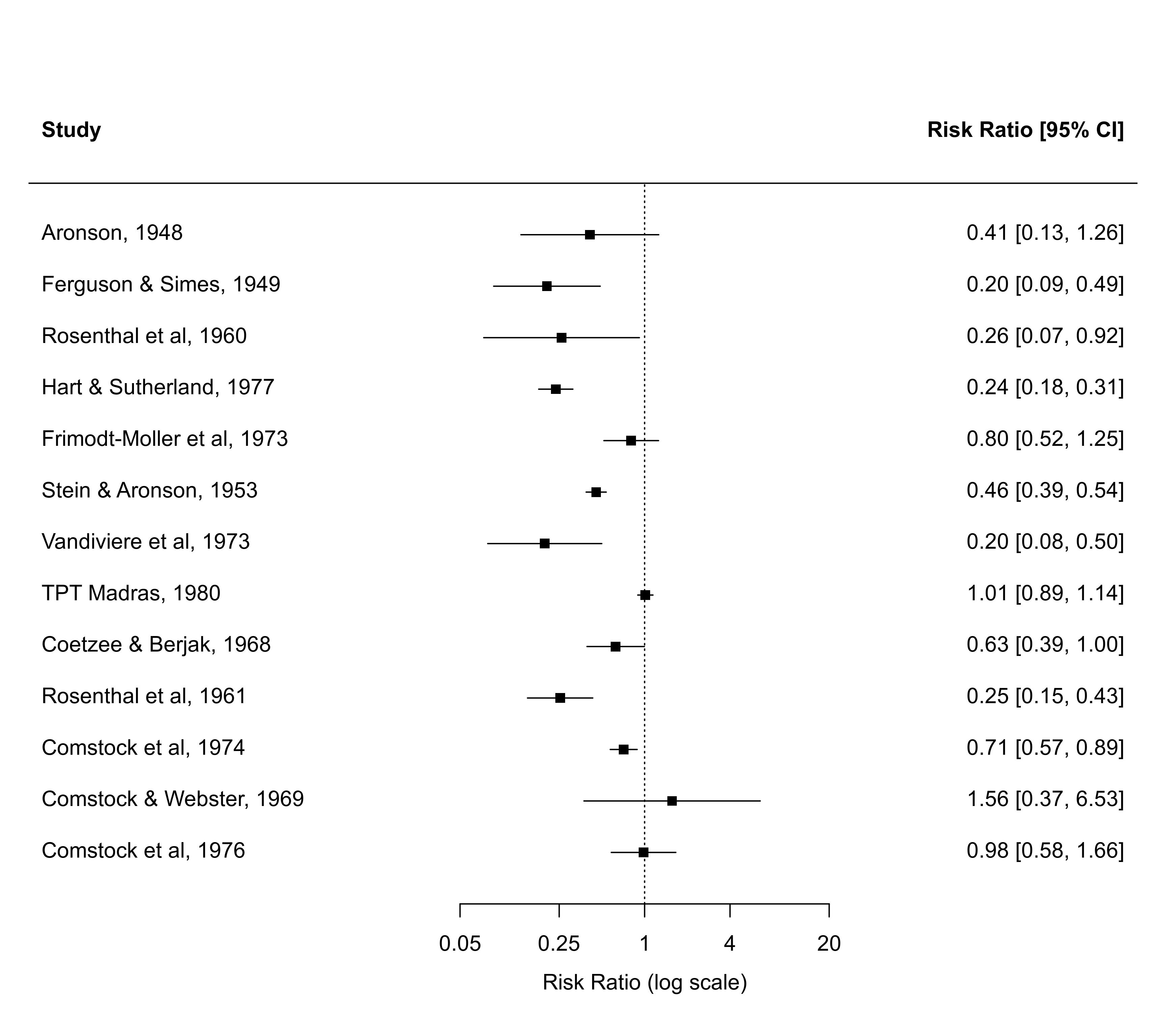
 ### and remove the vertical lines at the end of the CI bounds
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8), psize=1, efac=0))
### and remove the vertical lines at the end of the CI bounds
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8), psize=1, efac=0))
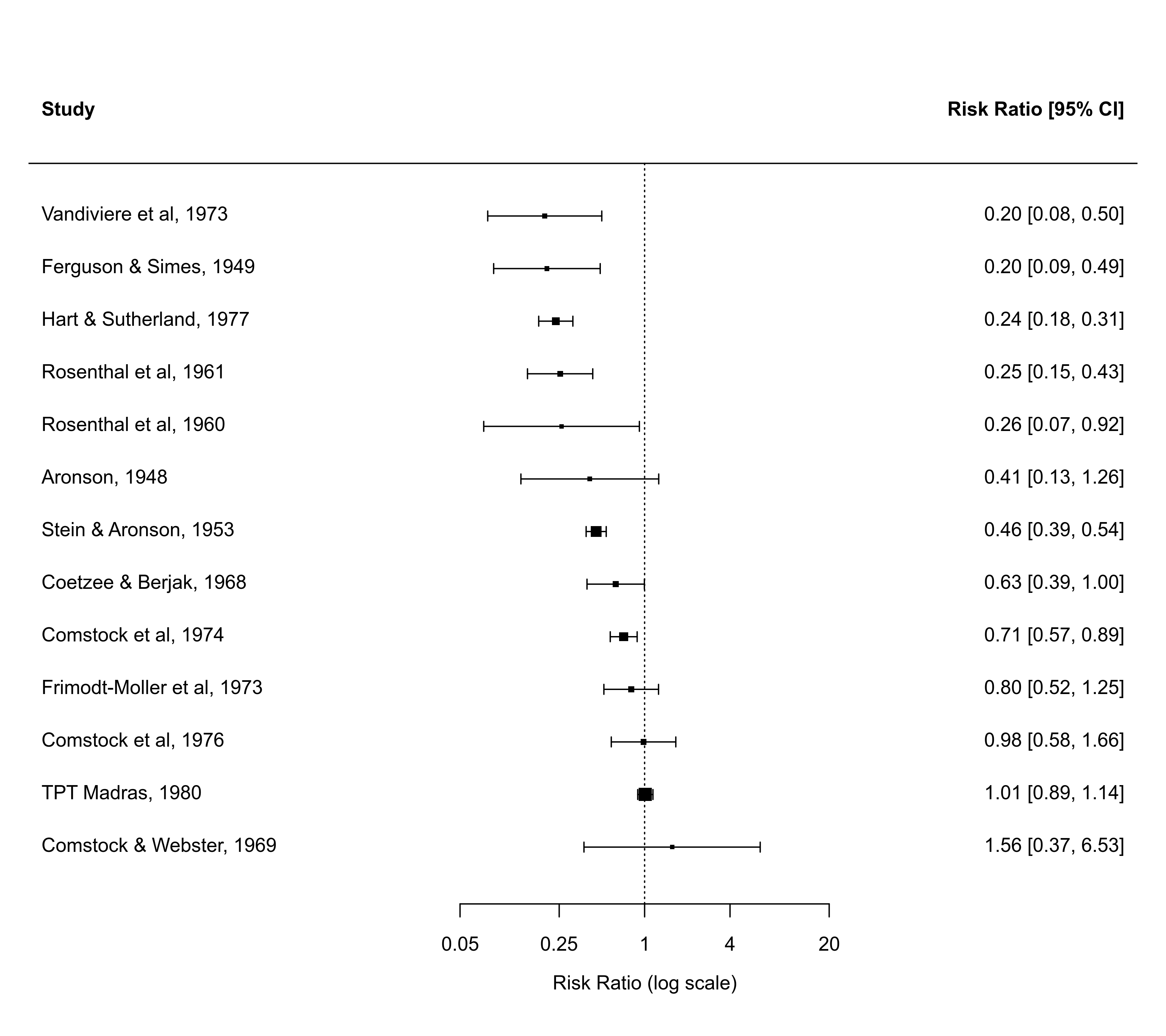
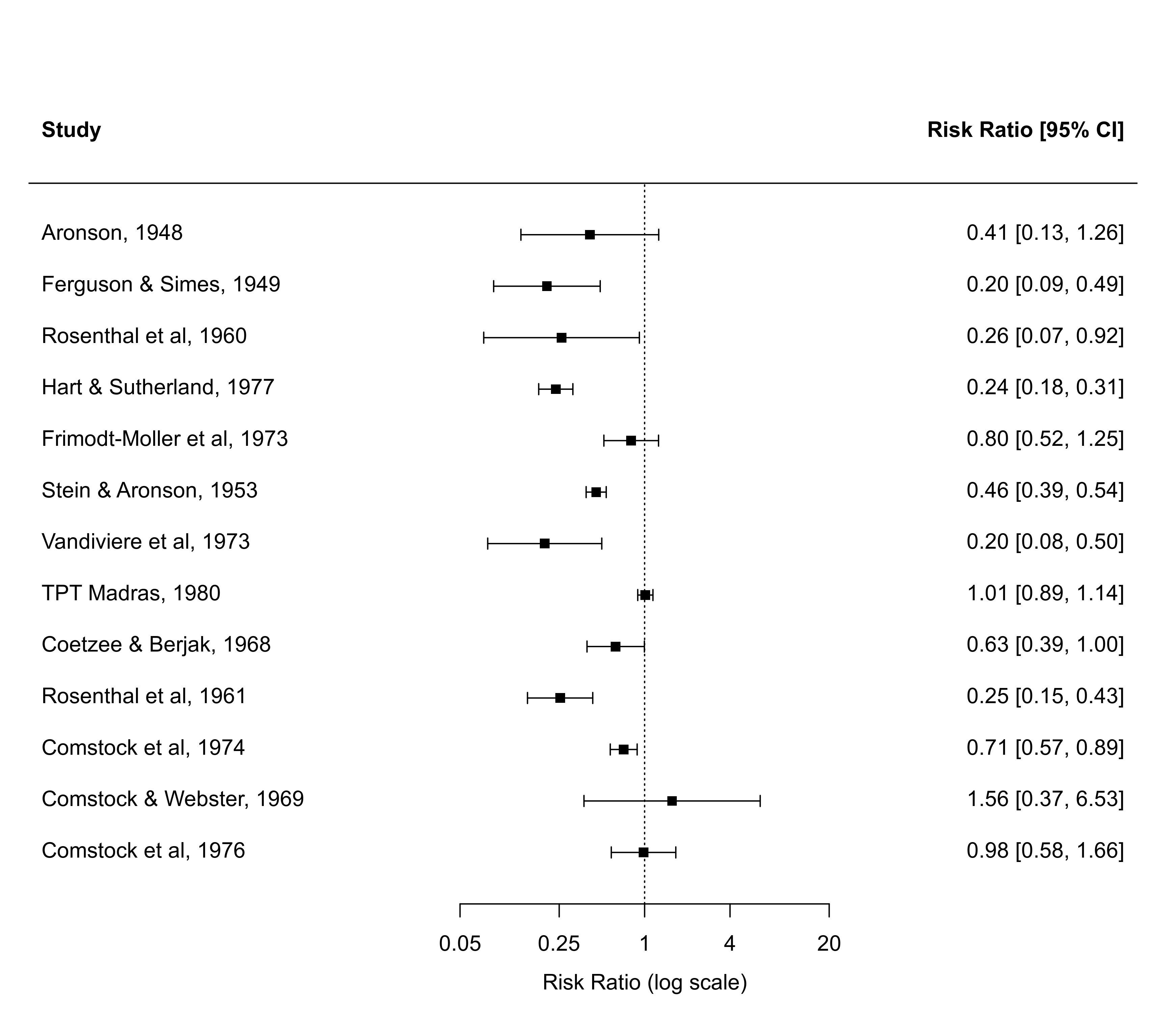
 ### forest plot of the observed risk ratios with studies ordered by the RRs
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8), order="obs"))
### forest plot of the observed risk ratios with studies ordered by the RRs
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8), order="obs"))
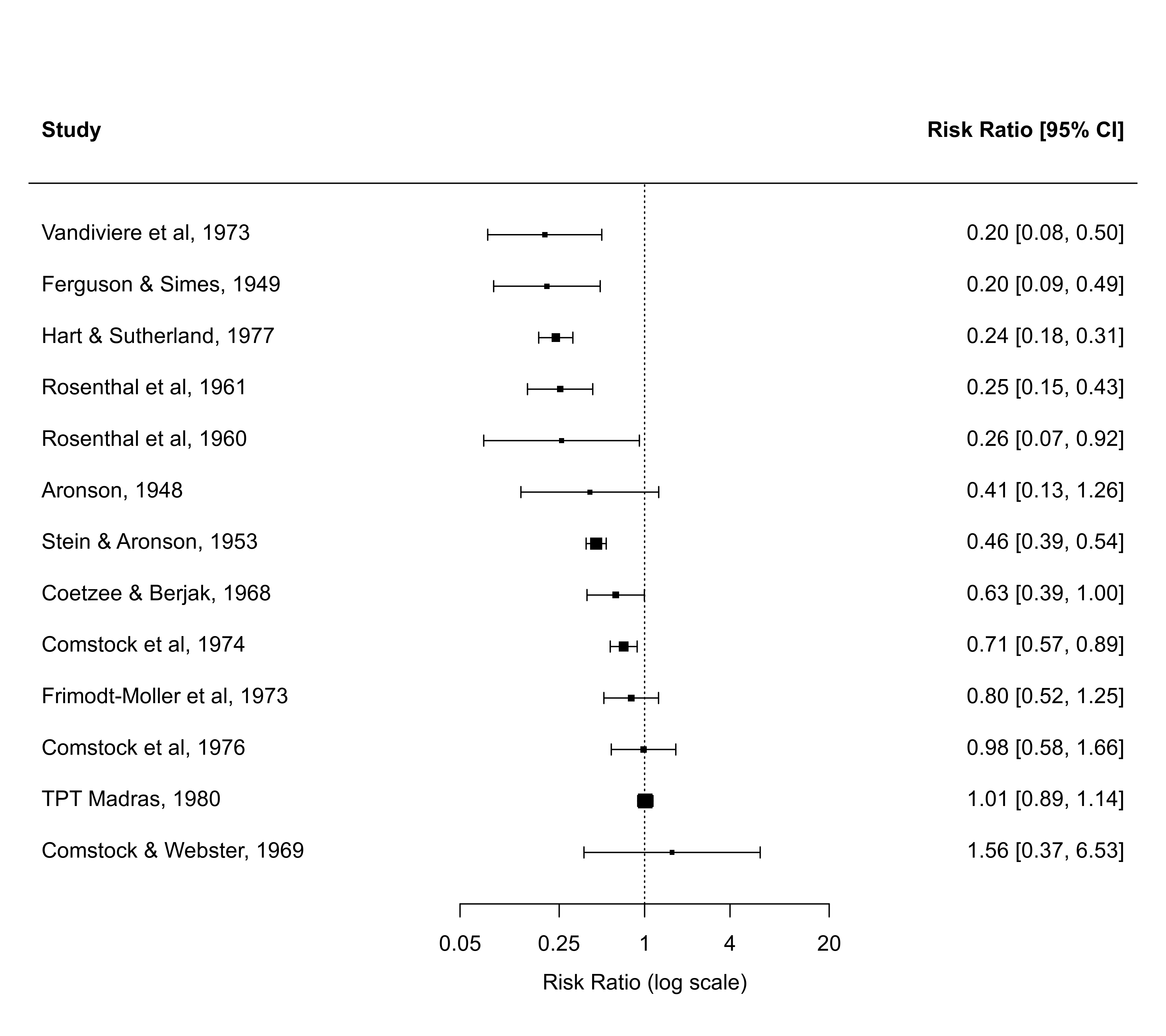 ### forest plot of the observed risk ratios with studies ordered by absolute latitude
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8), order=ablat))
### forest plot of the observed risk ratios with studies ordered by absolute latitude
with(dat, forest(yi, vi, atransf=exp, at=log(c(0.05,0.25,1,4,20)),
xlim=c(-10,8), order=ablat))
 ### see also examples for the forest.rma function
### see also examples for the forest.rma function