Studies on the Length of Hospital Stay of Stroke Patients
dat.normand1999.RdResults from 9 studies on the length of the hospital stay of stroke patients under specialized care and under conventional/routine (non-specialist) care.
dat.normand1999Format
The data frame contains the following columns:
| study | numeric | study number |
| source | character | source of data |
| n1i | numeric | number of patients under specialized care |
| m1i | numeric | mean length of stay (in days) under specialized care |
| sd1i | numeric | standard deviation of the length of stay under specialized care |
| n2i | numeric | number of patients under routine care |
| m2i | numeric | mean length of stay (in days) under routine care |
| sd2i | numeric | standard deviation of the length of stay under routine care |
Details
The 9 studies provide data in terms of the mean length of the hospital stay (in days) of stroke patients under specialized care and under conventional/routine (non-specialist) care. The goal of the meta-analysis was to examine the hypothesis whether specialist stroke unit care will result in a shorter length of hospitalization compared to routine management.
Source
Normand, S. T. (1999). Meta-analysis: Formulating, evaluating, combining, and reporting. Statistics in Medicine, 18(3), 321–359. https://doi.org/10.1002/(sici)1097-0258(19990215)18:3<321::aid-sim28>3.0.co;2-p
Concepts
medicine, raw mean differences, standardized mean differences
Examples
### copy data into 'dat' and examine data
dat <- dat.normand1999
dat
#> study source n1i m1i sd1i n2i m2i sd2i
#> 1 1 Edinburgh 155 55 47 156 75 64
#> 2 2 Orpington-Mild 31 27 7 32 29 4
#> 3 3 Orpington-Moderate 75 64 17 71 119 29
#> 4 4 Orpington-Severe 18 66 20 18 137 48
#> 5 5 Montreal-Home 8 14 8 13 18 11
#> 6 6 Montreal-Transfer 57 19 7 52 18 4
#> 7 7 Newcastle 34 52 45 33 41 34
#> 8 8 Umea 110 21 16 183 31 27
#> 9 9 Uppsala 60 30 27 52 23 20
### load metafor package
library(metafor)
### calculate mean differences and corresponding sampling variances
dat <- escalc(measure="MD", m1i=m1i, sd1i=sd1i, n1i=n1i, m2i=m2i, sd2i=sd2i, n2i=n2i, data=dat)
dat
#>
#> study source n1i m1i sd1i n2i m2i sd2i yi vi
#> 1 1 Edinburgh 155 55 47 156 75 64 -20.0000 40.5080
#> 2 2 Orpington-Mild 31 27 7 32 29 4 -2.0000 2.0806
#> 3 3 Orpington-Moderate 75 64 17 71 119 29 -55.0000 15.6984
#> 4 4 Orpington-Severe 18 66 20 18 137 48 -71.0000 150.2222
#> 5 5 Montreal-Home 8 14 8 13 18 11 -4.0000 17.3077
#> 6 6 Montreal-Transfer 57 19 7 52 18 4 1.0000 1.1673
#> 7 7 Newcastle 34 52 45 33 41 34 11.0000 94.5891
#> 8 8 Umea 110 21 16 183 31 27 -10.0000 6.3109
#> 9 9 Uppsala 60 30 27 52 23 20 7.0000 19.8423
#>
### meta-analysis of mean differences using a random-effects model
res <- rma(yi, vi, data=dat)
res
#>
#> Random-Effects Model (k = 9; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 684.6462 (SE = 359.7541)
#> tau (square root of estimated tau^2 value): 26.1657
#> I^2 (total heterogeneity / total variability): 98.97%
#> H^2 (total variability / sampling variability): 97.21
#>
#> Test for Heterogeneity:
#> Q(df = 8) = 238.9158, p-val < .0001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -15.1060 8.9466 -1.6885 0.0913 -32.6409 2.4289 .
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### meta-analysis of standardized mean differences using a random-effects model
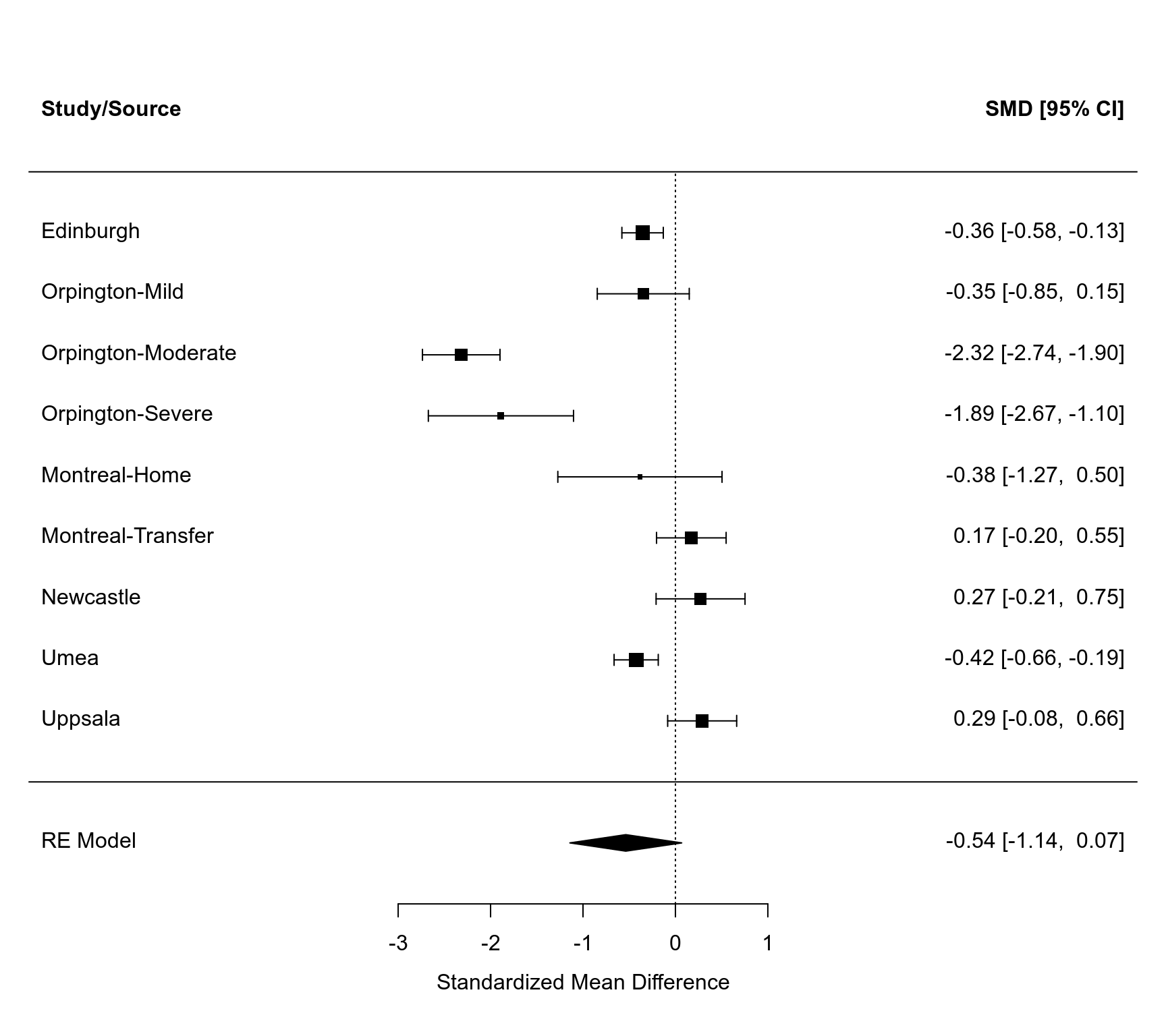
res <- rma(measure="SMD", m1i=m1i, sd1i=sd1i, n1i=n1i, m2i=m2i, sd2i=sd2i, n2i=n2i,
data=dat, slab=source)
res
#>
#> Random-Effects Model (k = 9; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.7908 (SE = 0.4281)
#> tau (square root of estimated tau^2 value): 0.8893
#> I^2 (total heterogeneity / total variability): 95.49%
#> H^2 (total variability / sampling variability): 22.20
#>
#> Test for Heterogeneity:
#> Q(df = 8) = 123.7293, p-val < .0001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.5371 0.3087 -1.7401 0.0818 -1.1421 0.0679 .
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### draw forest plot
forest(res, xlim=c(-7,5), alim=c(-3,1), header="Study/Source", top=2)
### calculate (log transformed) ratios of means and corresponding sampling variances
dat <- escalc(measure="ROM", m1i=m1i, sd1i=sd1i, n1i=n1i, m2i=m2i, sd2i=sd2i, n2i=n2i, data=dat)
dat
#>
#> study source n1i m1i sd1i n2i m2i sd2i yi vi
#> 1 1 Edinburgh 155 55 47 156 75 64 -0.3102 0.0094
#> 2 2 Orpington-Mild 31 27 7 32 29 4 -0.0715 0.0028
#> 3 3 Orpington-Moderate 75 64 17 71 119 29 -0.6202 0.0018
#> 4 4 Orpington-Severe 18 66 20 18 137 48 -0.7303 0.0119
#> 5 5 Montreal-Home 8 14 8 13 18 11 -0.2513 0.0695
#> 6 6 Montreal-Transfer 57 19 7 52 18 4 0.0541 0.0033
#> 7 7 Newcastle 34 52 45 33 41 34 0.2377 0.0429
#> 8 8 Umea 110 21 16 183 31 27 -0.3895 0.0094
#> 9 9 Uppsala 60 30 27 52 23 20 0.2657 0.0280
#>
### meta-analysis of the (log transformed) ratios of means using a random-effects model
res <- rma(yi, vi, data=dat)
res
#>
#> Random-Effects Model (k = 9; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.1080 (SE = 0.0620)
#> tau (square root of estimated tau^2 value): 0.3287
#> I^2 (total heterogeneity / total variability): 94.35%
#> H^2 (total variability / sampling variability): 17.71
#>
#> Test for Heterogeneity:
#> Q(df = 8) = 148.8186, p-val < .0001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.2184 0.1178 -1.8541 0.0637 -0.4492 0.0125 .
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
predict(res, transf=exp, digits=2)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 0.80 0.64 1.01 0.41 1.59
#>