Studies on the Effectiveness of Warfarin for Preventing Strokes
dat.hart1999.RdResults from 6 clinical trials examining the effectiveness of adjusted-dose warfarin for preventing strokes in patients with atrial fibrillation.
dat.hart1999Format
The data frame contains the following columns:
| trial | numeric | trial number |
| study | character | study name (abbreviated) |
| year | numeric | publication year |
| x1i | numeric | number of strokes in the warfarin group |
| n1i | numeric | number of patients in the warfarin group |
| t1i | numeric | total person-time (in years) in the warfarin group |
| x2i | numeric | number of strokes in the placebo/control group |
| n2i | numeric | number of patients in the placebo/control group |
| t2i | numeric | total person-time (in years) in the placebo/control group |
| compgrp | character | type of comparison group (placebo or control) |
| prevtype | character | type of prevention (primary or secondary) |
| trinr | character | target range for the international normalized ratio (INR) |
Details
The 6 studies provide data with respect to the number of strokes in the warfarin and the comparison (placebo or control) group. In addition, the number of patients and the total person-time (in years) is provided for the two groups. The goal of the meta-analysis was to examine the effectiveness of adjusted-dose warfarin for preventing strokes in patients with atrial fibrillation.
Source
Hart, R. G., Benavente, O., McBride, R., & Pearce, L. A. (1999). Antithrombotic therapy to prevent stroke in patients with atrial fibrillation: A meta-analysis. Annals of Internal Medicine, 131(7), 492–501. https://doi.org/10.7326/0003-4819-131-7-199910050-00003
Concepts
medicine, cardiology, incidence rates
Examples
### copy data into 'dat' and examine data
dat <- dat.hart1999
dat
#> trial study year x1i n1i t1i x2i n2i t2i compgrp prevtype trinr
#> 1 1 AFASAK 1989 9 335 413 19 336 398 placebo primary 2.8-4.2
#> 2 2 SPAF 1991 8 210 263 19 211 245 placebo primary 2.0-4.5
#> 3 3 BAATAF 1990 3 212 487 13 208 435 control primary 1.5-2.7
#> 4 4 CAFA 1991 6 187 237 9 191 241 placebo primary 2.0-3.0
#> 5 5 SPINAF 1992 7 281 489 23 290 483 placebo primary 1.4-2.8
#> 6 6 EAFT 1993 20 225 507 50 214 405 placebo secondary 2.5-4.0
### load metafor package
library(metafor)
### calculate log incidence rate ratios and corresponding sampling variances
dat <- escalc(measure="IRR", x1i=x1i, x2i=x2i, t1i=t1i, t2i=t2i, data=dat)
dat
#>
#> trial study year x1i n1i t1i x2i n2i t2i compgrp prevtype trinr yi vi
#> 1 1 AFASAK 1989 9 335 413 19 336 398 placebo primary 2.8-4.2 -0.7842 0.1637
#> 2 2 SPAF 1991 8 210 263 19 211 245 placebo primary 2.0-4.5 -0.9359 0.1776
#> 3 3 BAATAF 1990 3 212 487 13 208 435 control primary 1.5-2.7 -1.5793 0.4103
#> 4 4 CAFA 1991 6 187 237 9 191 241 placebo primary 2.0-3.0 -0.3887 0.2778
#> 5 5 SPINAF 1992 7 281 489 23 290 483 placebo primary 1.4-2.8 -1.2019 0.1863
#> 6 6 EAFT 1993 20 225 507 50 214 405 placebo secondary 2.5-4.0 -1.1409 0.0700
#>
### meta-analysis of log incidence rate ratios using a random-effects model
res <- rma(yi, vi, data=dat)
res
#>
#> Random-Effects Model (k = 6; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0 (SE = 0.0987)
#> tau (square root of estimated tau^2 value): 0
#> I^2 (total heterogeneity / total variability): 0.00%
#> H^2 (total variability / sampling variability): 1.00
#>
#> Test for Heterogeneity:
#> Q(df = 5) = 2.9625, p-val = 0.7058
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -1.0168 0.1635 -6.2206 <.0001 -1.3372 -0.6964 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### average incidence rate ratio with 95% CI
predict(res, transf=exp)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 0.3617 0.2626 0.4984 0.2626 0.4984
#>
### forest plot with extra annotations
par(mar=c(5,4,1,2))
forest(res, xlim=c(-11, 5), at=log(c(0.05, 0.25, 1, 4)), atransf=exp,
slab=paste0(study, " (", year, ")"),
ilab=cbind(paste(x1i, "/", t1i, sep=" "),
paste(x2i, "/", t2i, sep=" ")),
ilab.xpos=c(-6.5,-4), cex=0.85, header="Study (Year)")
op <- par(cex=0.85, font=2)
text(c(-6.5,-4), 8.5, c("Warfarin", "Control"))
text(c(-6.5,-4), 7.5, c("Strokes / PT", "Strokes / PT"))
segments(x0=-8, y0=8, x1=-2.75, y1=8)
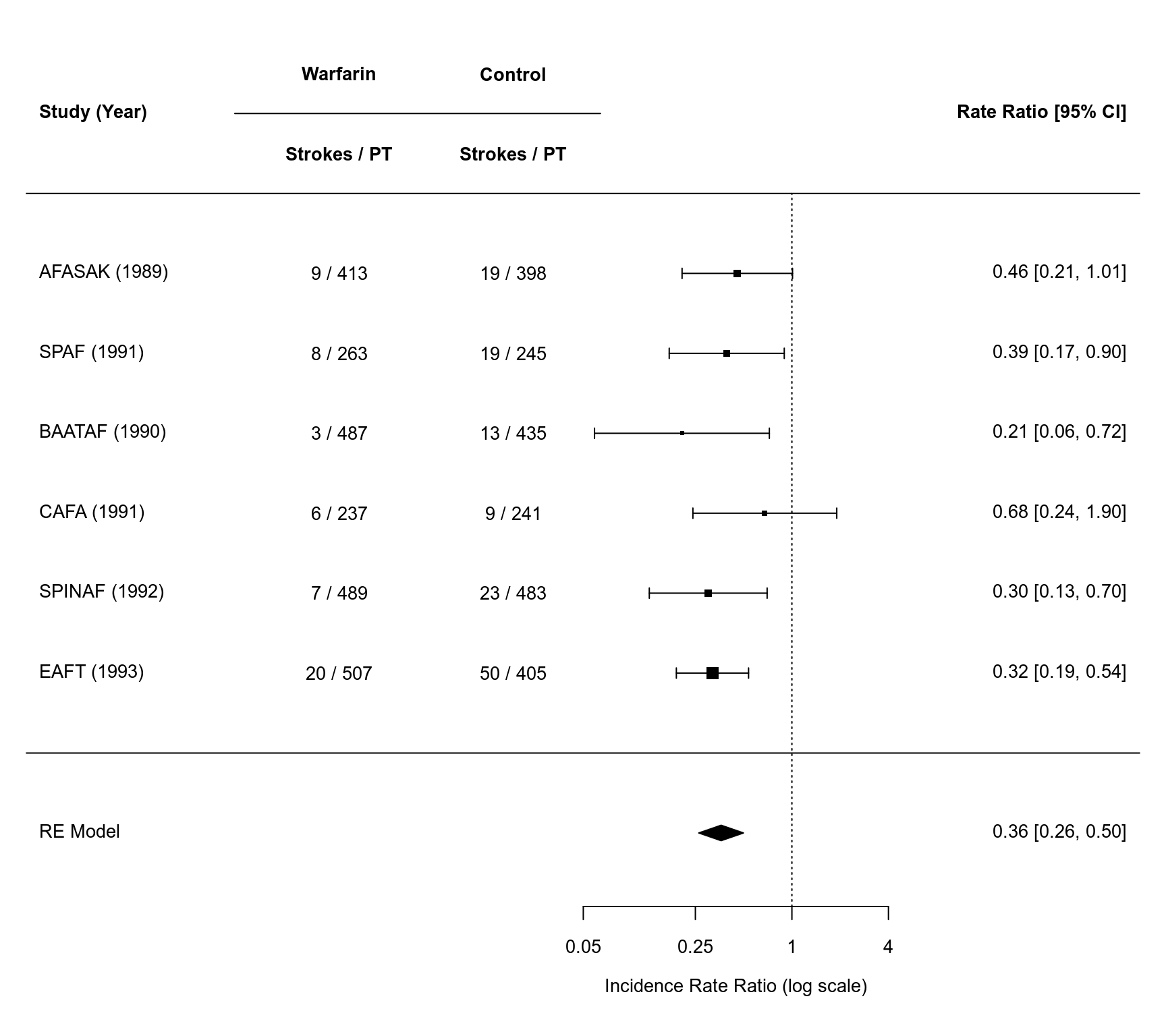par(op)
### meta-analysis of incidence rate differences using a random-effects model
res <- rma(measure="IRD", x1i=x1i, x2i=x2i, t1i=t1i, t2i=t2i, data=dat)
res
#>
#> Random-Effects Model (k = 6; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.0002 (SE = 0.0002)
#> tau (square root of estimated tau^2 value): 0.0139
#> I^2 (total heterogeneity / total variability): 50.75%
#> H^2 (total variability / sampling variability): 2.03
#>
#> Test for Heterogeneity:
#> Q(df = 5) = 10.1606, p-val = 0.0708
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.0339 0.0081 -4.1546 <.0001 -0.0498 -0.0179 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>