Studies on the Association Between the CASP8 -652 6N del Promoter Polymorphism and Breast Cancer Risk
dat.frank2008.RdResults from 4 case-control studies examining the association between the CASP8 -652 6N del promoter polymorphism and breast cancer risk.
dat.frank2008Format
The data frame contains the following columns:
| study | character | study identifier |
| bc.ins.ins | numeric | number of cases who have a homozygous insertion polymorphism |
| bc.ins.del | numeric | number of cases who have a heterozygous insertion/deletion polymorphism |
| bc.del.del | numeric | number of cases who have a homozygous deletion polymorphism |
| ct.ins.ins | numeric | number of controls who have a homozygous insertion polymorphism |
| ct.ins.del | numeric | number of controls who are heterozygous insertion/deletion polymorphism |
| ct.del.del | numeric | number of controls who have a homozygous deletion polymorphism |
Details
The 4 studies included in this dataset are case-control studies that have examined the association between the CASP8 -652 6N del promoter polymorphism and breast cancer risk. Breast cancer cases and controls were genotyped and either had a homozygous insertion, a heterozygous insertion/deletion, or a homozygous deletion polymorphism.
Ziegler et al. (2011) used the same dataset to illustrate the use of meta-analytic methods to examine deviations from Hardy-Weinberg equilibrium across multiple studies. The relative excess heterozygosity (REH) is the proposed measure for such a meta-analysis, which can be computed by setting measure="REH".
Source
Frank, B., Rigas, S. H., Bermejo, J. L., Wiestler, M., Wagner, K., Hemminki, K., Reed, M. W., Sutter, C., Wappenschmidt, B., Balasubramanian, S. P., Meindl, A., Kiechle, M., Bugert, P., Schmutzler, R. K., Bartram, C. R., Justenhoven, C., Ko, Y.-D., Brüning, T., Brauch, H., Hamann, U., Pharoah, P. P. D., Dunning, A. M., Pooley, K. A., Easton, D. F., Cox, A. & Burwinkel, B. (2008). The CASP8 -652 6N del promoter polymorphism and breast cancer risk: A multicenter study. Breast Cancer Research and Treatment, 111(1), 139–144. https://doi.org/10.1007/s10549-007-9752-z
References
Ziegler, A., Steen, K. V. & Wellek, S. (2011). Investigating Hardy-Weinberg equilibrium in case-control or cohort studies or meta-analysis. Breast Cancer Research and Treatment, 128(1), 197–201. https://doi.org/10.1007/s10549-010-1295-z
Concepts
medicine, oncology, genetics, odds ratios
Examples
### copy data into 'dat' and examine data
dat <- dat.frank2008
dat
#> study bc.ins.ins bc.ins.del bc.del.del ct.ins.ins ct.ins.del ct.del.del
#> 1 GFBCS 298 535 221 270 506 263
#> 2 SBCS 235 541 251 245 608 321
#> 3 GENICA 280 509 222 285 492 229
#> 4 SEARCH 1133 2115 1050 1149 2263 1062
### load metafor package
library(metafor)
### calculate log odds ratios comparing ins/del versus ins/ins
dat <- escalc(measure="OR", ai=bc.ins.del, bi=bc.ins.ins,
ci=ct.ins.del, di=ct.ins.ins, data=dat)
### fit random-effects model and get the pooled odds ratio (with 95% CI)
res <- rma(yi, vi, data=dat)
res
#>
#> Random-Effects Model (k = 4; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0 (SE = 0.0058)
#> tau (square root of estimated tau^2 value): 0
#> I^2 (total heterogeneity / total variability): 0.00%
#> H^2 (total variability / sampling variability): 1.00
#>
#> Test for Heterogeneity:
#> Q(df = 3) = 0.9329, p-val = 0.8175
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.0401 0.0395 -1.0155 0.3099 -0.1175 0.0373
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
predict(res, transf=exp, digits=2)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 0.96 0.89 1.04 0.89 1.04
#>
### calculate log odds ratios comparing del/del versus ins/ins
dat <- escalc(measure="OR", ai=bc.del.del, bi=bc.ins.ins,
ci=ct.del.del, di=ct.ins.ins, data=dat)
### fit random-effects model and get the pooled odds ratio (with 95% CI)
res <- rma(yi, vi, data=dat)
res
#>
#> Random-Effects Model (k = 4; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.0090 (SE = 0.0165)
#> tau (square root of estimated tau^2 value): 0.0950
#> I^2 (total heterogeneity / total variability): 45.66%
#> H^2 (total variability / sampling variability): 1.84
#>
#> Test for Heterogeneity:
#> Q(df = 3) = 5.4814, p-val = 0.1398
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.0988 0.0706 -1.4005 0.1614 -0.2372 0.0395
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
predict(res, transf=exp, digits=2)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 0.91 0.79 1.04 0.72 1.14
#>
### calculate log odds ratios comparing ins/del+del/del versus ins/ins
dat <- escalc(measure="OR", ai=bc.ins.del+bc.del.del, bi=bc.ins.ins,
ci=ct.ins.del+ct.del.del, di=ct.ins.ins, data=dat)
### fit random-effects model and get the pooled odds ratio (with 95% CI)
res <- rma(yi, vi, data=dat)
res
#>
#> Random-Effects Model (k = 4; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0 (SE = 0.0052)
#> tau (square root of estimated tau^2 value): 0
#> I^2 (total heterogeneity / total variability): 0.00%
#> H^2 (total variability / sampling variability): 1.00
#>
#> Test for Heterogeneity:
#> Q(df = 3) = 1.6413, p-val = 0.6501
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.0481 0.0373 -1.2921 0.1963 -0.1211 0.0249
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
predict(res, transf=exp, digits=2)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 0.95 0.89 1.03 0.89 1.03
#>
############################################################################
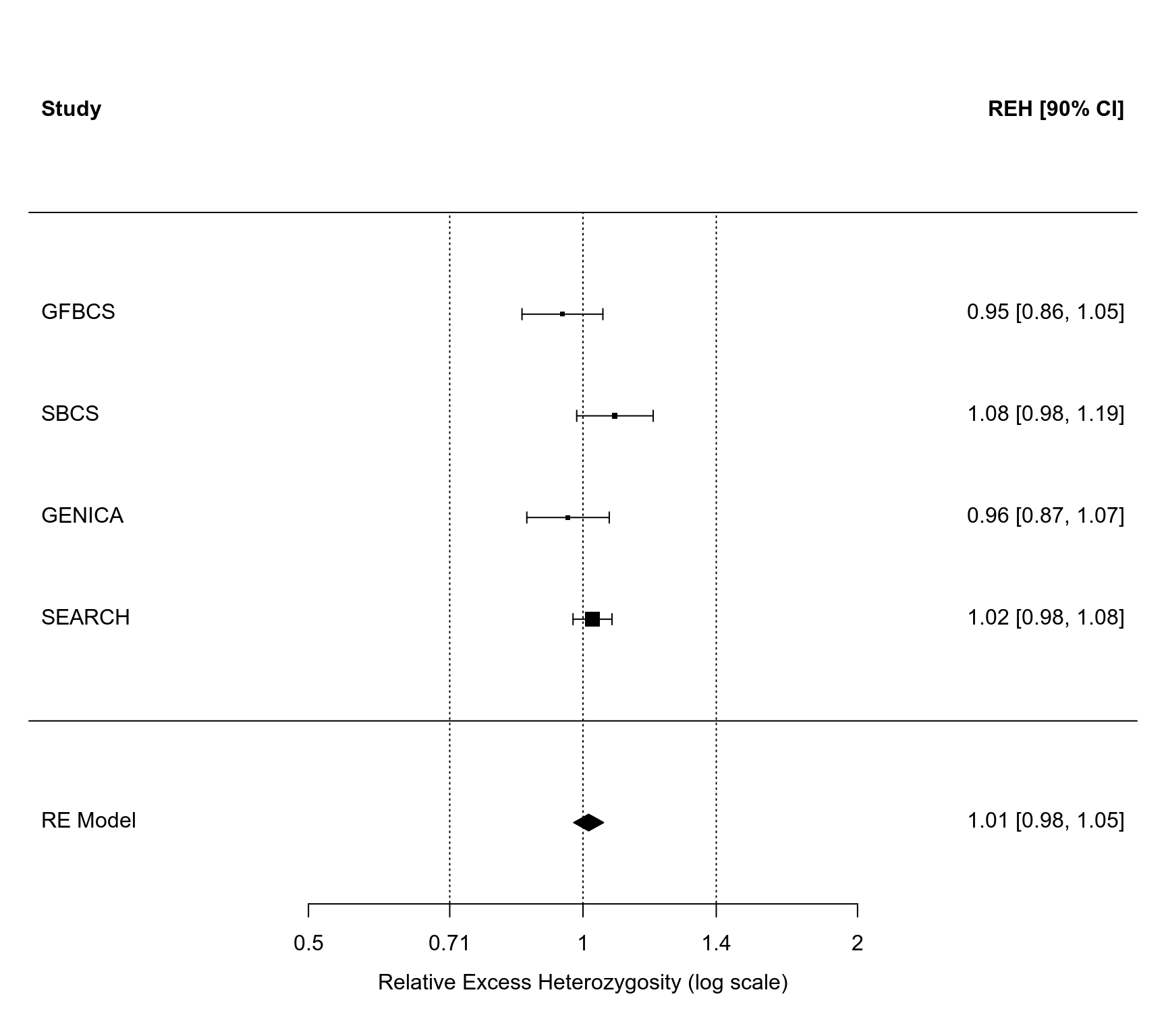
### compute the relative excess heterozygosity in the controls
dat <- escalc(measure="REH", ai=ct.ins.ins, bi=ct.ins.del, ci=ct.del.del,
slab=study, data=dat)
### fit random-effects model and get the pooled REH value (with 90% CI)
res <- rma(yi, vi, data=dat, level=90)
res
#>
#> Random-Effects Model (k = 4; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.0000 (SE = 0.0019)
#> tau (square root of estimated tau^2 value): 0.0011
#> I^2 (total heterogeneity / total variability): 0.05%
#> H^2 (total variability / sampling variability): 1.00
#>
#> Test for Heterogeneity:
#> Q(df = 3) = 3.2001, p-val = 0.3618
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> 0.0143 0.0228 0.6242 0.5325 -0.0233 0.0518
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
predict(res, transf=exp, digits=2)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 1.01 0.98 1.05 0.98 1.05
#>
### draw forest plot
forest(res, atransf=exp, xlim=c(-1.4,1.4), at=log(c(0.5,5/7,1,7/5,2)))
segments(log(5/7), -2, log(5/7), res$k+1, lty="dotted")
segments(log(7/5), -2, log(7/5), res$k+1, lty="dotted")