Studies on Radiation Therapy with or without Adjuvant Chemotherapy in Patients with Malignant Gliomas
dat.fine1993.RdResults from 17 trials comparing post-operative radiation therapy with and without adjuvant chemotherapy in patients with malignant gliomas.
dat.fine1993Format
The data frame contains the following columns:
| study | numeric | study number |
| nei | numeric | sample size in the experimental group receiving radiotherapy plus adjuvant chemotherapy |
| nci | numeric | sample size in the control group receiving radiotherapy alone |
| e1i | numeric | number of survivors at 6 months in the experimental group |
| c1i | numeric | number of survivors at 6 months in the control group |
| e2i | numeric | number of survivors at 12 months in the experimental group |
| c2i | numeric | number of survivors at 12 months in the control group |
| e3i | numeric | number of survivors at 18 months in the experimental group |
| c3i | numeric | number of survivors at 18 months in the control group |
| e4i | numeric | number of survivors at 24 months in the experimental group |
| c4i | numeric | number of survivors at 24 months in the control group |
Details
The 17 trials report the post-operative survival of patients with malignant gliomas receiving either radiation therapy with adjuvant chemotherapy or radiation therapy alone. Survival was assessed at 6, 12, 18, and 24 months in all but one study (which assessed survival only at 12 and at 24 months).
The data were reconstructed by Trikalinos and Olkin (2012) based on Table 2 in Fine et al. (1993) and Table 3 in Dear (1994). The data can be used to illustrate how a meta-analysis can be conducted of effect sizes reported at multiple time points using a multivariate model.
Source
Dear, K. B. G. (1994). Iterative generalized least squares for meta-analysis of survival data at multiple times. Biometrics, 50(4), 989–1002. https://doi.org/10.2307/2533438
Trikalinos, T. A., & Olkin, I. (2012). Meta-analysis of effect sizes reported at multiple time points: A multivariate approach. Clinical Trials, 9(5), 610–620. https://doi.org/10.1177/1740774512453218
References
Fine, H. A., Dear, K. B., Loeffler, J. S., Black, P. M., & Canellos, G. P. (1993). Meta-analysis of radiation therapy with and without adjuvant chemotherapy for malignant gliomas in adults. Cancer, 71(8), 2585–2597. https://doi.org/10.1002/1097-0142(19930415)71:8<2585::aid-cncr2820710825>3.0.co;2-s
Concepts
medicine, oncology, odds ratios, longitudinal models
Examples
### copy data into 'dat' and examine data
dat <- dat.fine1993
dat
#> study nei nci e1i c1i e2i c2i e3i c3i e4i c4i
#> 1 1 19 22 16 20 11 12 4 8 4 3
#> 2 2 34 35 22 22 18 12 15 8 15 6
#> 3 3 72 68 44 40 21 15 10 3 3 0
#> 4 4 22 20 19 12 14 5 5 4 2 3
#> 5 5 70 32 62 27 42 13 26 6 15 5
#> 6 6 183 94 130 65 80 33 47 14 30 11
#> 7 7 26 50 24 30 13 18 5 10 3 9
#> 8 8 61 55 51 44 37 30 19 19 11 15
#> 9 9 36 25 30 17 23 12 13 4 10 4
#> 10 10 45 35 43 35 19 14 8 4 6 0
#> 11 11 246 208 169 139 106 76 67 42 51 35
#> 12 12 386 141 279 97 170 46 97 21 73 8
#> 13 13 59 32 56 30 34 17 21 9 20 7
#> 14 14 45 15 42 10 18 3 9 1 9 1
#> 15 15 14 18 14 18 13 14 12 13 9 12
#> 16 16 26 19 21 15 12 10 6 4 5 1
#> 17 17 74 75 NA NA 42 40 NA NA 23 30
### load metafor package
library(metafor)
### calculate log(ORs) and sampling variances for each time point
dat <- escalc(measure="OR", ai=e1i, n1i=nei, ci=c1i, n2i=nci, data=dat, var.names=c("y1i","v1i"))
dat <- escalc(measure="OR", ai=e2i, n1i=nei, ci=c2i, n2i=nci, data=dat, var.names=c("y2i","v2i"))
dat <- escalc(measure="OR", ai=e3i, n1i=nei, ci=c3i, n2i=nci, data=dat, var.names=c("y3i","v3i"))
dat <- escalc(measure="OR", ai=e4i, n1i=nei, ci=c4i, n2i=nci, data=dat, var.names=c("y4i","v4i"))
### calculate the covariances (equations in Appendix of Trikalinos & Olkin, 2012)
dat$v12i <- with(dat, nei / (e1i * (nei - e2i)) + nci / (c1i * (nci - c2i)))
dat$v13i <- with(dat, nei / (e1i * (nei - e3i)) + nci / (c1i * (nci - c3i)))
dat$v14i <- with(dat, nei / (e1i * (nei - e4i)) + nci / (c1i * (nci - c4i)))
dat$v23i <- with(dat, nei / (e2i * (nei - e3i)) + nci / (c2i * (nci - c3i)))
dat$v24i <- with(dat, nei / (e2i * (nei - e4i)) + nci / (c2i * (nci - c4i)))
dat$v34i <- with(dat, nei / (e3i * (nei - e4i)) + nci / (c3i * (nci - c4i)))
### create dataset in long format
dat.long <- data.frame(study=rep(1:nrow(dat), each=4), time=1:4,
yi=c(t(dat[c("y1i","y2i","y3i","y4i")])),
vi=c(t(dat[c("v1i","v2i","v3i","v4i")])))
### var-cov matrices of the studies
V <- lapply(split(dat, dat$study),
function(x) matrix(c( x$v1i, x$v12i, x$v13i, x$v14i,
x$v12i, x$v2i, x$v23i, x$v24i,
x$v13i, x$v23i, x$v3i, x$v34i,
x$v14i, x$v24i, x$v34i, x$v4i), nrow=4, ncol=4, byrow=TRUE))
### remove rows for the missing time points in study 17
dat.long <- na.omit(dat.long)
### remove corresponding rows/columns from var-cov matrix
V[[17]] <- V[[17]][c(2,4),c(2,4)]
### make a copy of V
Vc <- V
### replace any (near) singular var-cov matrices with ridge corrected versions
repl.Vi <- function(Vi) {
res <- eigen(Vi)
if (any(res$values <= 0.08)) {
round(res$vectors %*% diag(res$values + 0.08) %*% t(res$vectors), 12)
} else {
Vi
}
}
Vc <- lapply(Vc, repl.Vi)
### do not correct var-cov matrix of study 17
Vc[[17]] <- V[[17]]
### construct block diagonal matrix
Vc <- bldiag(Vc)
### multivariate fixed-effects model
res <- rma.mv(yi, Vc, mods = ~ 0 + factor(time), method="FE", data=dat.long)
print(res, digits=3)
#>
#> Multivariate Meta-Analysis Model (k = 66; method: FE)
#>
#> Variance Components: none
#>
#> Test for Residual Heterogeneity:
#> QE(df = 62) = 62.447, p-val = 0.460
#>
#> Test of Moderators (coefficients 1:4):
#> QM(df = 4) = 15.631, p-val = 0.004
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> factor(time)1 0.251 0.143 1.755 0.079 -0.029 0.532 .
#> factor(time)2 0.428 0.114 3.742 <.001 0.204 0.652 ***
#> factor(time)3 0.343 0.134 2.560 0.010 0.080 0.606 *
#> factor(time)4 0.281 0.138 2.035 0.042 0.010 0.552 *
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### multivariate random-effects model with heteroscedastic AR(1) structure for the true effects
res <- rma.mv(yi, Vc, mods = ~ 0 + factor(time), random = ~ time | study,
struct="HAR", data=dat.long, control=list(optimizer="hjk"))
print(res, digits=3)
#>
#> Multivariate Meta-Analysis Model (k = 66; method: REML)
#>
#> Variance Components:
#>
#> outer factor: study (nlvls = 17)
#> inner factor: time (nlvls = 4)
#>
#> estim sqrt k.lvl fixed level
#> tau^2.1 0.000 0.000 16 no 1
#> tau^2.2 0.000 0.015 17 no 2
#> tau^2.3 0.029 0.172 16 no 3
#> tau^2.4 0.197 0.443 17 no 4
#> rho 1.000 no
#>
#> Test for Residual Heterogeneity:
#> QE(df = 62) = 62.447, p-val = 0.460
#>
#> Test of Moderators (coefficients 1:4):
#> QM(df = 4) = 14.555, p-val = 0.006
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> factor(time)1 0.254 0.143 1.772 0.076 -0.027 0.534 .
#> factor(time)2 0.408 0.115 3.536 <.001 0.182 0.634 ***
#> factor(time)3 0.365 0.145 2.521 0.012 0.081 0.650 *
#> factor(time)4 0.351 0.187 1.878 0.060 -0.015 0.718 .
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
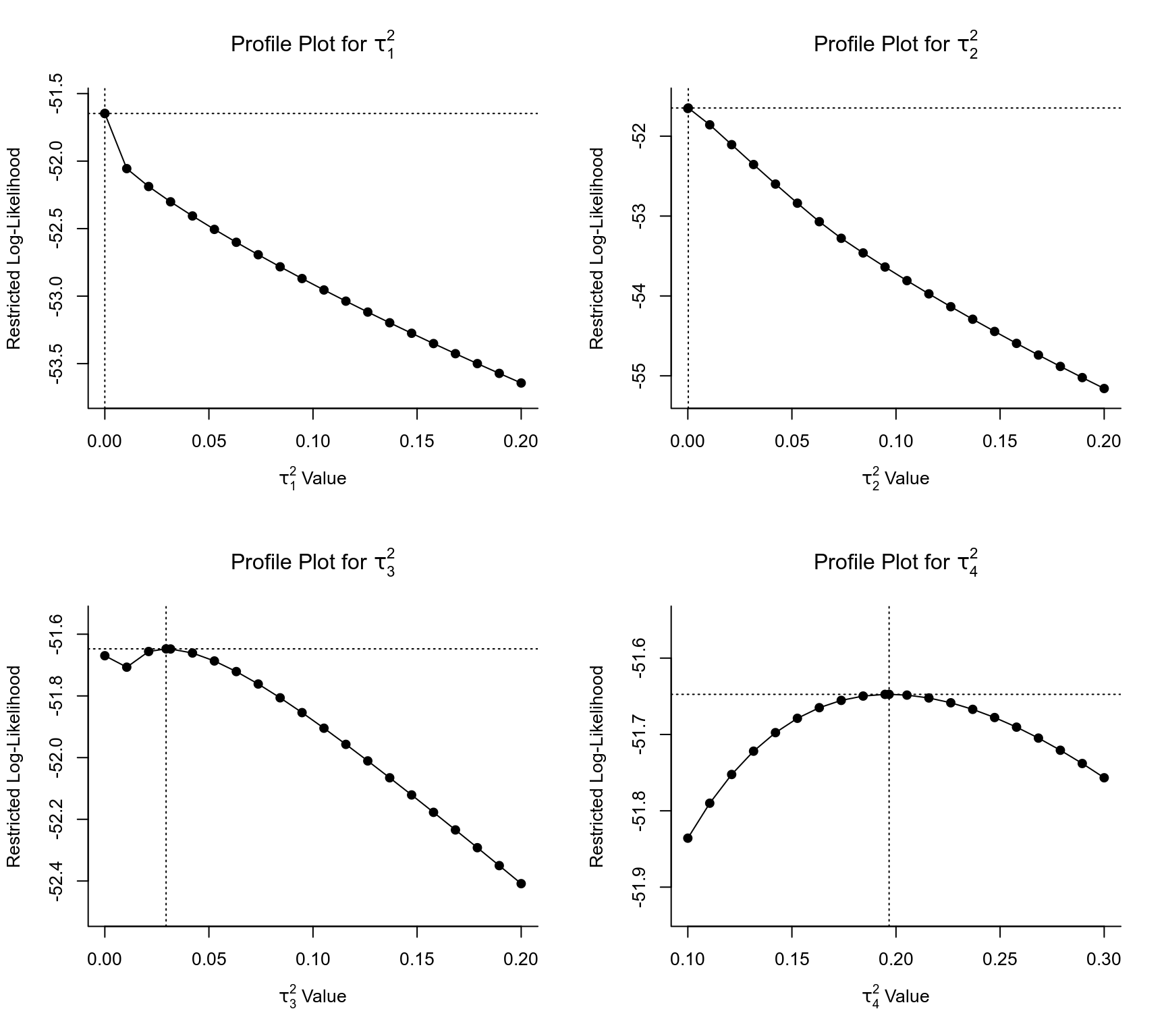
### profile the variance components
par(mfrow=c(2,2))
profile(res, tau2=1, xlim=c( 0, 0.2))
profile(res, tau2=2, xlim=c( 0, 0.2))
profile(res, tau2=3, xlim=c( 0, 0.2))
profile(res, tau2=4, xlim=c(0.1, 0.3))
 ### profile the autocorrelation coefficient
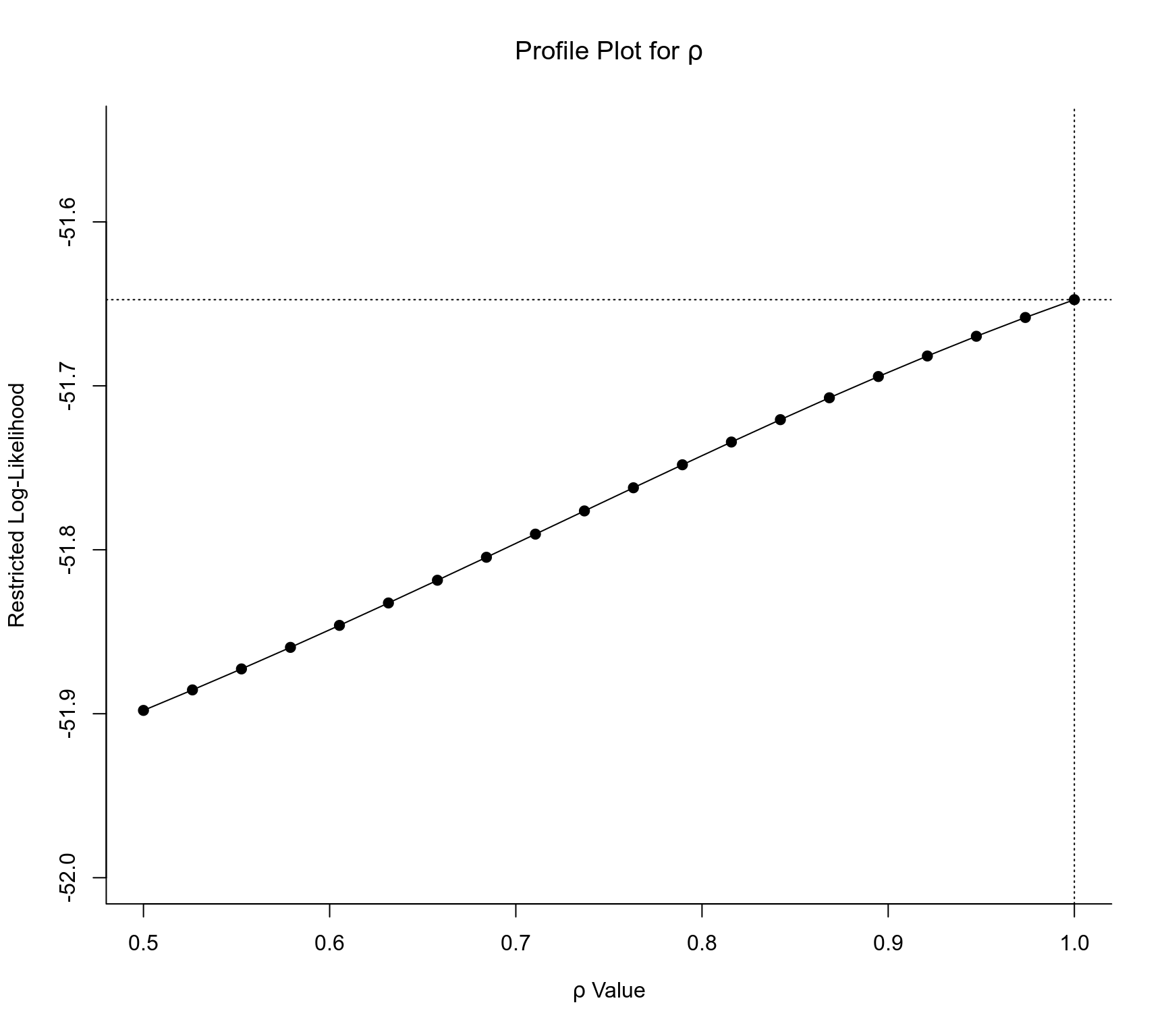
par(mfrow=c(1,1))
profile(res, rho=1)
### profile the autocorrelation coefficient
par(mfrow=c(1,1))
profile(res, rho=1)