Studies on the Effectiveness of the BCG Vaccine Against Tuberculosis
dat.colditz1994.RdResults from 13 studies examining the effectiveness of the Bacillus Calmette-Guerin (BCG) vaccine against tuberculosis.
dat.colditz1994Format
The data frame contains the following columns:
| trial | numeric | trial number |
| author | character | author(s) |
| year | numeric | publication year |
| tpos | numeric | number of TB positive cases in the treated (vaccinated) group |
| tneg | numeric | number of TB negative cases in the treated (vaccinated) group |
| cpos | numeric | number of TB positive cases in the control (non-vaccinated) group |
| cneg | numeric | number of TB negative cases in the control (non-vaccinated) group |
| ablat | numeric | absolute latitude of the study location (in degrees) |
| alloc | character | method of treatment allocation (random, alternate, or systematic assignment) |
Details
The 13 studies provide data in terms of \(2 \times 2\) tables in the form:
| TB positive | TB negative | |
| vaccinated group | tpos | tneg |
| control group | cpos | cneg |
The goal of the meta-analysis was to examine the overall effectiveness of the BCG vaccine for preventing tuberculosis and to examine moderators that may potentially influence the size of the effect.
The dataset has been used in several publications to illustrate meta-analytic methods (see ‘References’).
Source
Colditz, G. A., Brewer, T. F., Berkey, C. S., Wilson, M. E., Burdick, E., Fineberg, H. V., & Mosteller, F. (1994). Efficacy of BCG vaccine in the prevention of tuberculosis: Meta-analysis of the published literature. Journal of the American Medical Association, 271(9), 698–702. https://doi.org/10.1001/jama.1994.03510330076038
References
Berkey, C. S., Hoaglin, D. C., Mosteller, F., & Colditz, G. A. (1995). A random-effects regression model for meta-analysis. Statistics in Medicine, 14(4), 395–411. https://doi.org/10.1002/sim.4780140406
van Houwelingen, H. C., Arends, L. R., & Stijnen, T. (2002). Advanced methods in meta-analysis: Multivariate approach and meta-regression. Statistics in Medicine, 21(4), 589–624. https://doi.org/10.1002/sim.1040
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://doi.org/10.18637/jss.v036.i03
Concepts
medicine, risk ratios, meta-regression
Examples
### copy data into 'dat' and examine data
dat <- dat.colditz1994
dat
#> trial author year tpos tneg cpos cneg ablat alloc
#> 1 1 Aronson 1948 4 119 11 128 44 random
#> 2 2 Ferguson & Simes 1949 6 300 29 274 55 random
#> 3 3 Rosenthal et al 1960 3 228 11 209 42 random
#> 4 4 Hart & Sutherland 1977 62 13536 248 12619 52 random
#> 5 5 Frimodt-Moller et al 1973 33 5036 47 5761 13 alternate
#> 6 6 Stein & Aronson 1953 180 1361 372 1079 44 alternate
#> 7 7 Vandiviere et al 1973 8 2537 10 619 19 random
#> 8 8 TPT Madras 1980 505 87886 499 87892 13 random
#> 9 9 Coetzee & Berjak 1968 29 7470 45 7232 27 random
#> 10 10 Rosenthal et al 1961 17 1699 65 1600 42 systematic
#> 11 11 Comstock et al 1974 186 50448 141 27197 18 systematic
#> 12 12 Comstock & Webster 1969 5 2493 3 2338 33 systematic
#> 13 13 Comstock et al 1976 27 16886 29 17825 33 systematic
### load metafor package
library(metafor)
### calculate log risk ratios and corresponding sampling variances
dat <- escalc(measure="RR", ai=tpos, bi=tneg,
ci=cpos, di=cneg, data=dat,
slab=paste0(author, ", ", year))
dat
#>
#> trial author year tpos tneg cpos cneg ablat alloc yi vi
#> 1 1 Aronson 1948 4 119 11 128 44 random -0.8893 0.3256
#> 2 2 Ferguson & Simes 1949 6 300 29 274 55 random -1.5854 0.1946
#> 3 3 Rosenthal et al 1960 3 228 11 209 42 random -1.3481 0.4154
#> 4 4 Hart & Sutherland 1977 62 13536 248 12619 52 random -1.4416 0.0200
#> 5 5 Frimodt-Moller et al 1973 33 5036 47 5761 13 alternate -0.2175 0.0512
#> 6 6 Stein & Aronson 1953 180 1361 372 1079 44 alternate -0.7861 0.0069
#> 7 7 Vandiviere et al 1973 8 2537 10 619 19 random -1.6209 0.2230
#> 8 8 TPT Madras 1980 505 87886 499 87892 13 random 0.0120 0.0040
#> 9 9 Coetzee & Berjak 1968 29 7470 45 7232 27 random -0.4694 0.0564
#> 10 10 Rosenthal et al 1961 17 1699 65 1600 42 systematic -1.3713 0.0730
#> 11 11 Comstock et al 1974 186 50448 141 27197 18 systematic -0.3394 0.0124
#> 12 12 Comstock & Webster 1969 5 2493 3 2338 33 systematic 0.4459 0.5325
#> 13 13 Comstock et al 1976 27 16886 29 17825 33 systematic -0.0173 0.0714
#>
### random-effects model
res <- rma(yi, vi, data=dat)
res
#>
#> Random-Effects Model (k = 13; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.3132 (SE = 0.1664)
#> tau (square root of estimated tau^2 value): 0.5597
#> I^2 (total heterogeneity / total variability): 92.22%
#> H^2 (total variability / sampling variability): 12.86
#>
#> Test for Heterogeneity:
#> Q(df = 12) = 152.2330, p-val < .0001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> -0.7145 0.1798 -3.9744 <.0001 -1.0669 -0.3622 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### average risk ratio with 95% CI
predict(res, transf=exp)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 0.4894 0.3441 0.6962 0.1546 1.5490
#>
### mixed-effects model with absolute latitude and publication year as moderators
res <- rma(yi, vi, mods = ~ ablat + year, data=dat)
res
#>
#> Mixed-Effects Model (k = 13; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of residual heterogeneity): 0.1108 (SE = 0.0845)
#> tau (square root of estimated tau^2 value): 0.3328
#> I^2 (residual heterogeneity / unaccounted variability): 71.98%
#> H^2 (unaccounted variability / sampling variability): 3.57
#> R^2 (amount of heterogeneity accounted for): 64.63%
#>
#> Test for Residual Heterogeneity:
#> QE(df = 10) = 28.3251, p-val = 0.0016
#>
#> Test of Moderators (coefficients 2:3):
#> QM(df = 2) = 12.2043, p-val = 0.0022
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> intrcpt -3.5455 29.0959 -0.1219 0.9030 -60.5724 53.4814
#> ablat -0.0280 0.0102 -2.7371 0.0062 -0.0481 -0.0080 **
#> year 0.0019 0.0147 0.1299 0.8966 -0.0269 0.0307
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### predicted average risk ratios for 10-60 degrees absolute latitude
### holding the publication year constant at 1970
predict(res, newmods=cbind(seq(from=10, to=60, by=10), 1970), transf=exp)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 1 0.9345 0.5833 1.4973 0.4179 2.0899
#> 2 0.7062 0.5149 0.9686 0.3421 1.4579
#> 3 0.5337 0.4196 0.6789 0.2663 1.0697
#> 4 0.4033 0.2956 0.5502 0.1958 0.8306
#> 5 0.3048 0.1916 0.4848 0.1369 0.6787
#> 6 0.2303 0.1209 0.4386 0.0921 0.5761
#>
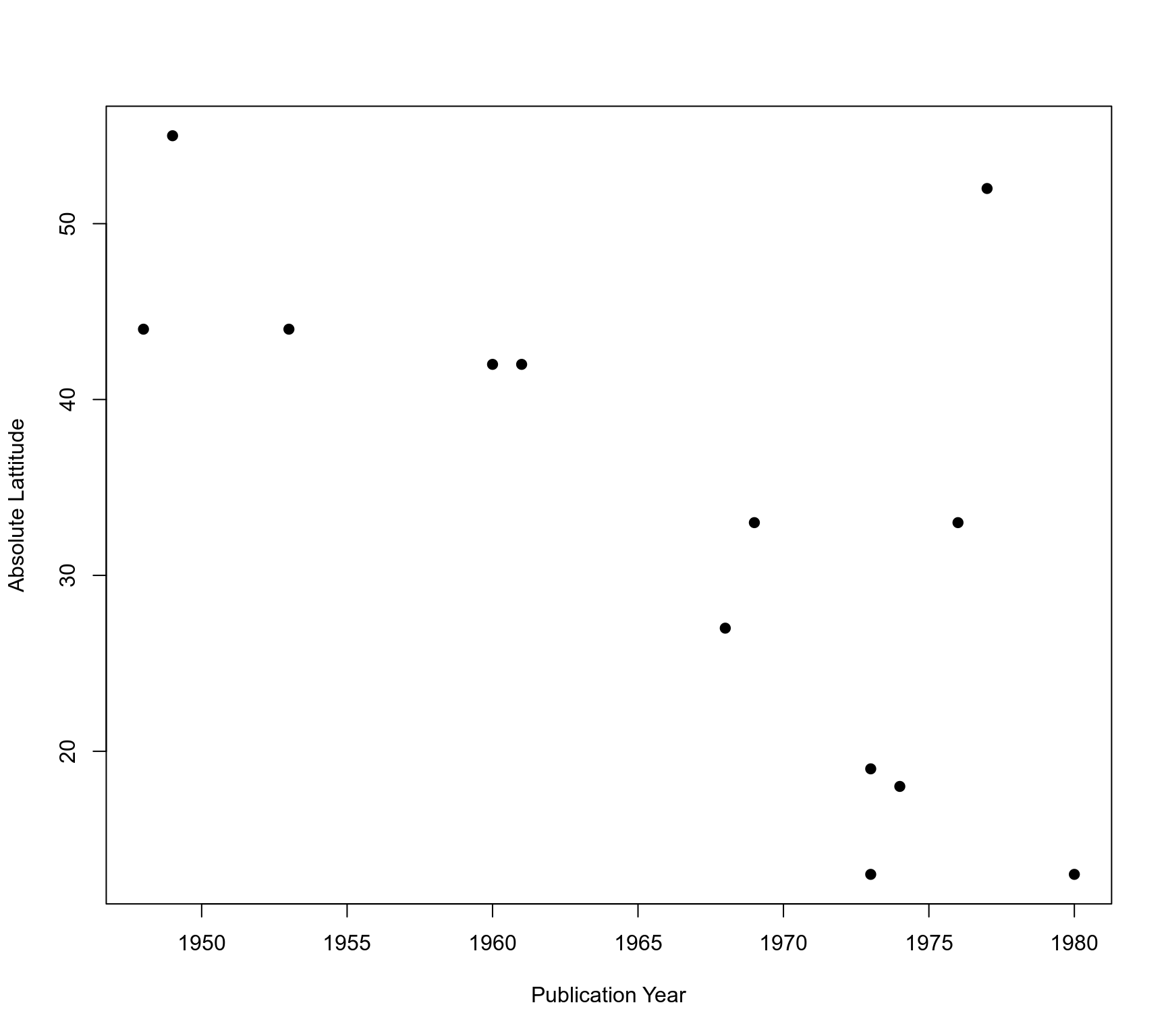
### note: the interpretation of the results is difficult because absolute
### latitude and publication year are strongly correlated (the more recent
### studies were conducted closer to the equator)
plot(ablat ~ year, data=dat, pch=19, xlab="Publication Year", ylab="Absolute Lattitude")
 cor(dat$ablat, dat$year)
#> [1] -0.6630572
cor(dat$ablat, dat$year)
#> [1] -0.6630572