Studies on the Effectiveness of Coaching for the SAT
dat.kalaian1996.RdResults from studies examining the effectiveness of coaching on the performance on the Scholastic Aptitude Test (SAT).
dat.kalaian1996Format
The data frame contains the following columns:
| id | numeric | row (effect) id |
| study | character | study identifier |
| year | numeric | publication year |
| n1i | numeric | number of participants in the coached group |
| n2i | numeric | number of participants in the uncoached group |
| outcome | character | subtest (verbal or math) |
| yi | numeric | standardized mean difference |
| vi | numeric | corresponding sampling variance |
| hrs | numeric | hours of coaching |
| ets | numeric | study conducted by the Educational Testing Service (ETS) (0 = no, 1 = yes) |
| homework | numeric | assignment of homework outside of the coaching course (0 = no, 1 = yes) |
| type | numeric | study type (1 = randomized study, 2 = matched study, 3 = nonequivalent comparison study) |
Details
The effectiveness of coaching for the Scholastic Aptitude Test (SAT) has been examined in numerous studies. This dataset contains standardized mean differences comparing the performance of a coached versus uncoached group on the verbal and/or math subtest of the SAT. Studies may report a standardized mean difference for the verbal subtest, the math subtest, or both. In the latter case, the two standardized mean differences are not independent (since they were measured in the same group of subjects). The number of hours of coaching (variable hrs), whether the study was conducted by the Educational Testing Service (variable ets), whether homework was assigned outside of the coaching course (variable homework), and the study type (variable type) may be potential moderators of the treatment effect.
Note
The dataset was obtained from Table 1 in Kalaian and Raudenbush (1996). However, there appear to be some inconsistencies between the data in the table and those that were actually used for the analyses (see ‘Examples’).
Source
Kalaian, H. A., & Raudenbush, S. W. (1996). A multivariate mixed linear model for meta-analysis. Psychological Methods, 1(3), 227–235. https://doi.org/10.1037/1082-989X.1.3.227
Concepts
education, standardized mean differences, multivariate models, meta-regression
Examples
### copy data into 'dat' and examine data
dat <- dat.kalaian1996
head(dat, 12)
#> id study year n1i n2i outcome yi vi hrs ets homework type
#> 1 1 Alderman & Powers (A) 1980 28 22 verbal 0.22 0.0817 7.0 1 1 1
#> 2 2 Alderman & Powers (B) 1980 39 40 verbal 0.09 0.0507 10.0 1 1 1
#> 3 3 Alderman & Powers (C) 1980 22 17 verbal 0.14 0.1045 10.5 1 1 1
#> 4 4 Alderman & Powers (D) 1980 48 43 verbal 0.14 0.0442 10.0 1 1 1
#> 5 5 Alderman & Powers (E) 1980 25 74 verbal -0.01 0.0535 6.0 1 1 1
#> 6 6 Alderman & Powers (F) 1980 37 35 verbal 0.14 0.0557 5.0 1 1 1
#> 7 7 Alderman & Powers (G) 1980 24 70 verbal 0.18 0.0561 11.0 1 1 1
#> 8 8 Alderman & Powers (H) 1980 16 19 verbal 0.01 0.1151 45.0 1 1 1
#> 9 9 Evans & Pike (A) 1973 145 129 verbal 0.13 0.0147 21.0 1 1 1
#> 10 10 Evans & Pike (A) 1973 145 129 math 0.12 0.0147 21.0 1 1 1
#> 11 11 Evans & Pike (B) 1973 72 129 verbal 0.25 0.0218 21.0 1 1 1
#> 12 12 Evans & Pike (B) 1973 72 129 math 0.06 0.0216 21.0 1 1 1
### load metafor package
library(metafor)
### check ranges
range(dat$yi[dat$outcome == "verbal"]) # -0.35 to 0.74 according to page 230
#> [1] -0.38 0.74
range(dat$yi[dat$outcome == "math"]) # -0.53 to 0.60 according to page 231
#> [1] -0.53 0.60
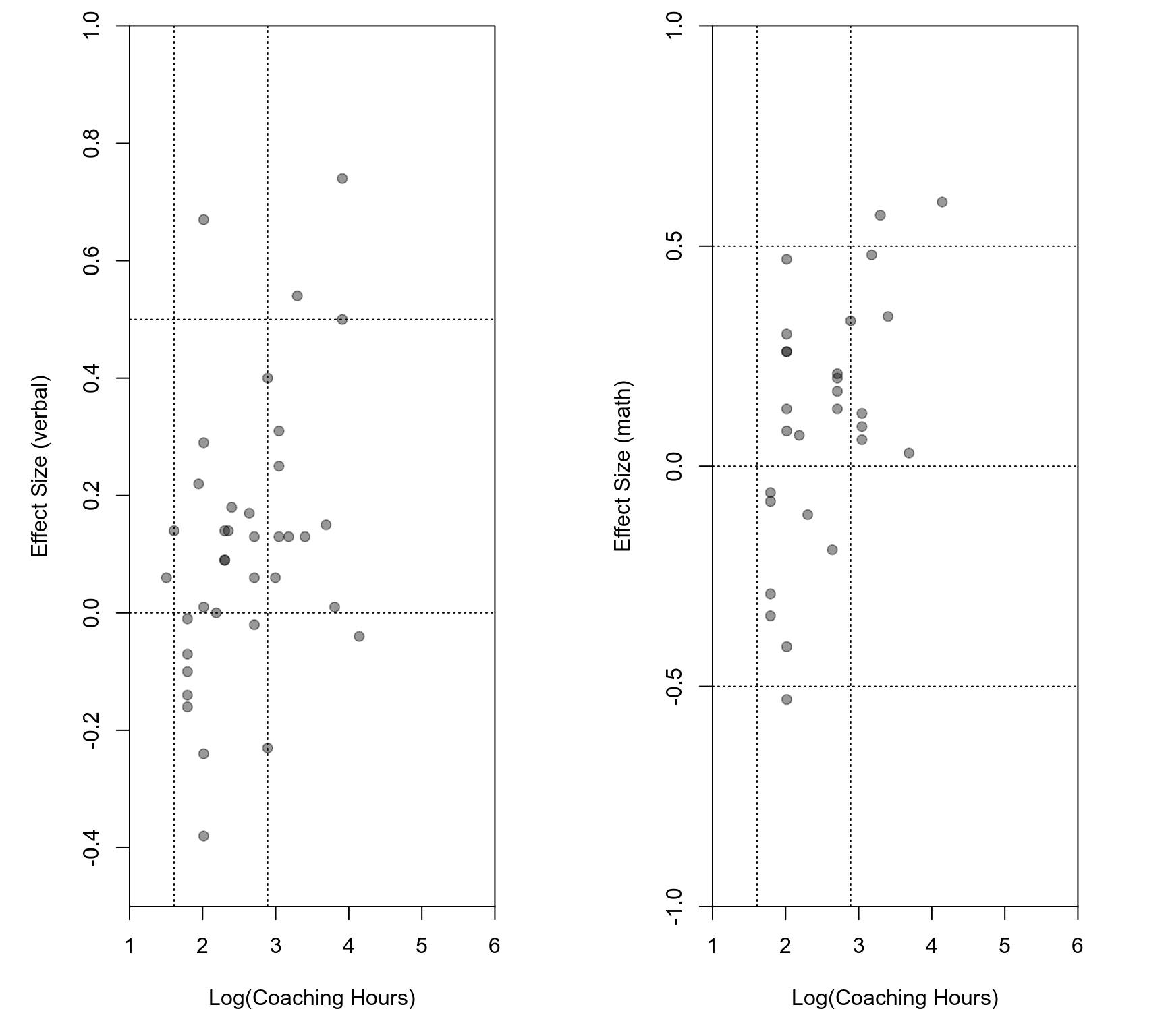
### comparing this with Figure 1 in the paper reveals some discrepancies
par(mfrow=c(1,2), mar=c(5,5,1,3.4))
plot(log(dat$hrs[dat$outcome == "verbal"]), dat$yi[dat$outcome == "verbal"],
pch=19, col=rgb(0,0,0,.4), xlab="Log(Coaching Hours)", ylab="Effect Size (verbal)",
xlim=c(1,6), ylim=c(-0.5,1), xaxs="i", yaxs="i")
abline(h=c(-0.5,0,0.5), lty="dotted")
abline(v=log(c(5,18)), lty="dotted")
plot(log(dat$hrs[dat$outcome == "math"]), dat$yi[dat$outcome == "math"],
pch=19, col=rgb(0,0,0,.4), xlab="Log(Coaching Hours)", ylab="Effect Size (math)",
xlim=c(1,6), ylim=c(-1.0,1), xaxs="i", yaxs="i")
abline(h=c(-0.5,0,0.5), lty="dotted")
abline(v=log(c(5,18)), lty="dotted")
### construct variance-covariance matrix assuming rho = 0.66 for effect sizes
### corresponding to the 'verbal' and 'math' outcome types
V <- vcalc(vi, cluster=study, type=outcome, data=dat, rho=0.66)
### fit multivariate random-effects model
res <- rma.mv(yi, V, mods = ~ 0 + outcome,
random = ~ outcome | study, struct="UN",
data=dat, digits=3)
res
#>
#> Multivariate Meta-Analysis Model (k = 67; method: REML)
#>
#> Variance Components:
#>
#> outer factor: study (nlvls = 47)
#> inner factor: outcome (nlvls = 2)
#>
#> estim sqrt k.lvl fixed level
#> tau^2.1 0.012 0.110 29 no math
#> tau^2.2 0.003 0.051 38 no verbal
#>
#> rho.math rho.vrbl math vrbl
#> math 1 - 20
#> verbal -1.000 1 no -
#>
#> Test for Residual Heterogeneity:
#> QE(df = 65) = 72.163, p-val = 0.253
#>
#> Test of Moderators (coefficients 1:2):
#> QM(df = 2) = 18.129, p-val < .001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> outcomemath 0.138 0.043 3.178 0.001 0.053 0.223 **
#> outcomeverbal 0.117 0.034 3.460 <.001 0.051 0.183 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### test whether the effect differs for the math and verbal subtest
anova(res, X=c(1,-1))
#>
#> Hypothesis:
#> 1: outcomemath - outcomeverbal = 0
#>
#> Results:
#> estimate se zval pval
#> 1: 0.021 0.049 0.433 0.665
#>
#> Test of Hypothesis:
#> QM(df = 1) = 0.187, p-val = 0.665
#>
### log-transform and mean center the hours of coaching variable
dat$loghrs <- log(dat$hrs) - mean(log(dat$hrs), na.rm=TRUE)
### fit multivariate model with log(hrs) as moderator
res <- rma.mv(yi, V, mods = ~ 0 + outcome + outcome:loghrs,
random = ~ outcome | study, struct="UN",
data=dat, digits=3)
#> Warning: 2 rows with NAs omitted from model fitting.
res
#>
#> Multivariate Meta-Analysis Model (k = 65; method: REML)
#>
#> Variance Components:
#>
#> outer factor: study (nlvls = 46)
#> inner factor: outcome (nlvls = 2)
#>
#> estim sqrt k.lvl fixed level
#> tau^2.1 0.015 0.123 28 no math
#> tau^2.2 0.001 0.037 37 no verbal
#>
#> rho.math rho.vrbl math vrbl
#> math 1 - 19
#> verbal -1.000 1 no -
#>
#> Test for Residual Heterogeneity:
#> QE(df = 61) = 67.958, p-val = 0.252
#>
#> Test of Moderators (coefficients 1:4):
#> QM(df = 4) = 23.646, p-val < .001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> outcomemath 0.102 0.049 2.088 0.037 0.006 0.197 *
#> outcomeverbal 0.110 0.035 3.166 0.002 0.042 0.178 **
#> outcomemath:loghrs 0.169 0.073 2.335 0.020 0.027 0.312 *
#> outcomeverbal:loghrs 0.049 0.046 1.068 0.285 -0.041 0.139
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### fit model with tau2 = 0 for outcome verbal (which also constrains rho = 0)
res <- rma.mv(yi, V, mods = ~ 0 + outcome + outcome:loghrs,
random = ~ outcome | study, struct="UN", tau2=c(NA,0),
data=dat, digits=3)
#> Warning: 2 rows with NAs omitted from model fitting.
res
#>
#> Multivariate Meta-Analysis Model (k = 65; method: REML)
#>
#> Variance Components:
#>
#> outer factor: study (nlvls = 46)
#> inner factor: outcome (nlvls = 2)
#>
#> estim sqrt k.lvl fixed level
#> tau^2.1 0.021 0.145 28 no math
#> tau^2.2 0.000 0.000 37 yes verbal
#>
#> rho.math rho.vrbl math vrbl
#> math 1 - 19
#> verbal 0.000 1 yes -
#>
#> Test for Residual Heterogeneity:
#> QE(df = 61) = 67.958, p-val = 0.252
#>
#> Test of Moderators (coefficients 1:4):
#> QM(df = 4) = 23.350, p-val < .001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> outcomemath 0.107 0.051 2.103 0.035 0.007 0.207 *
#> outcomeverbal 0.114 0.034 3.396 <.001 0.048 0.180 ***
#> outcomemath:loghrs 0.187 0.076 2.463 0.014 0.038 0.337 *
#> outcomeverbal:loghrs 0.060 0.044 1.357 0.175 -0.027 0.147
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>