Studies on Deep-Brain Stimulation in Patients with Parkinson's disease

Results from 46 studies examining the effects of deep-brain stimulation on motor skills of patients with Parkinson's disease.

dat.ishak2007

Format

The data frame contains the following columns:

studycharacter(first) author and year
y1inumericobserved mean difference at 3 months
v1inumericsampling variance of the mean difference at 3 months
y2inumericobserved mean difference at 6 months
v2inumericsampling variance of the mean difference at 6 months
y3inumericobserved mean difference at 12 months
v3inumericsampling variance of the mean difference at 12 months
y4inumericobserved mean difference at the long-term follow-up
v4inumericsampling variance of the mean difference at the long-term follow-up
mdurnumericmean disease duration (in years)
mbasenumericmean baseline UPDRS score

Details

Deep-brain stimulation (DBS), which is delivered through thin surgically implanted wires in specific areas of the brain and controlled by the patient, is meant to provide relief of the debilitating symptoms of Parkinson's disease. The dataset includes the results from 46 studies examining the effects of DBS of the subthalamic nucleus on motor functioning, measured with the Unified Parkinson's Disease Rating Scale (UPDRS). The effect size measure for this meta-analysis was the mean difference of the scores while the stimulator is active and the baseline scores (before implantation of the stimulator). Since lower scores on the UPDRS indicate better functioning, negative numbers indicate improvements in motor skills. Effects were generally measured at 3, 6, and 12 months after implantation of the stimulator, with some studies also including a further long-term follow-up. However, the number of measurements differed between studies - hence the missing data on some of the measurement occasions.

Since the same patients were followed over time within a study, effect size estimates from multiple measurement occasions are likely to be correlated. A multivariate model accounting for the correlation in the effects can be used to meta-analyze these data. A difficulty with this approach is the lack of information about the correlation of the measurements over time in the individual studies. The approach taken by Ishak et al. (2007) was to assume an autoregressive (AR1) structure for the estimates within the individual studies. In addition, the correlation in the true effects was modeled, again using an autoregressive structure.

Source

Ishak, K. J., Platt, R. W., Joseph, L., Hanley, J. A., & Caro, J. J. (2007). Meta-analysis of longitudinal studies. Clinical Trials, 4(5), 525–539. https://doi.org/10.1177/1740774507083567

Concepts

medicine, raw mean differences, longitudinal models

Examples

### copy data into 'dat' and examine data
dat <- dat.ishak2007
head(dat, 5)
#> 
#>               study   y1i  v1i   y2i   v2i   y3i v3i y4i v4i mdur mbase 
#> 1    Alegret (2001) -33.4 14.3    NA    NA    NA  NA  NA  NA 16.1  53.6 
#> 2 Barichella (2003) -20.0  7.3    NA    NA -30.0 5.7  NA  NA 13.5  45.3 
#> 3     Berney (2002) -21.1  7.3    NA    NA    NA  NA  NA  NA 13.6  45.6 
#> 4   Burchiel (1999) -20.0  8.0 -20.0   8.0 -18.0 5.0  NA  NA 13.6  48.0 
#> 5       Chen (2003)    NA   NA -32.9 125.0    NA  NA  NA  NA 12.1  65.7 
#> 

### load metafor package
library(metafor)

### create long format dataset
dat <- reshape(dat, direction="long", idvar="study", v.names=c("yi","vi"),
               varying=list(c(2,4,6,8), c(3,5,7,9)))
dat <- dat[order(study, time),]

### remove missing measurement occasions from dat.long
dat <- dat[!is.na(yi),]
rownames(dat) <- NULL
head(dat, 8)
#> 
#>               study mdur mbase time    yi    vi 
#> 1    Alegret (2001) 16.1  53.6    1 -33.4  14.3 
#> 2 Barichella (2003) 13.5  45.3    1 -20.0   7.3 
#> 3 Barichella (2003) 13.5  45.3    3 -30.0   5.7 
#> 4     Berney (2002) 13.6  45.6    1 -21.1   7.3 
#> 5   Burchiel (1999) 13.6  48.0    1 -20.0   8.0 
#> 6   Burchiel (1999) 13.6  48.0    2 -20.0   8.0 
#> 7   Burchiel (1999) 13.6  48.0    3 -18.0   5.0 
#> 8       Chen (2003) 12.1  65.7    2 -32.9 125.0 
#> 

### construct the full (block diagonal) V matrix with an AR(1) structure
### assuming an autocorrelation of 0.97 as estimated by Ishak et al. (2007)
V <- vcalc(vi, cluster=study, time1=time, phi=0.97, data=dat)

### plot data
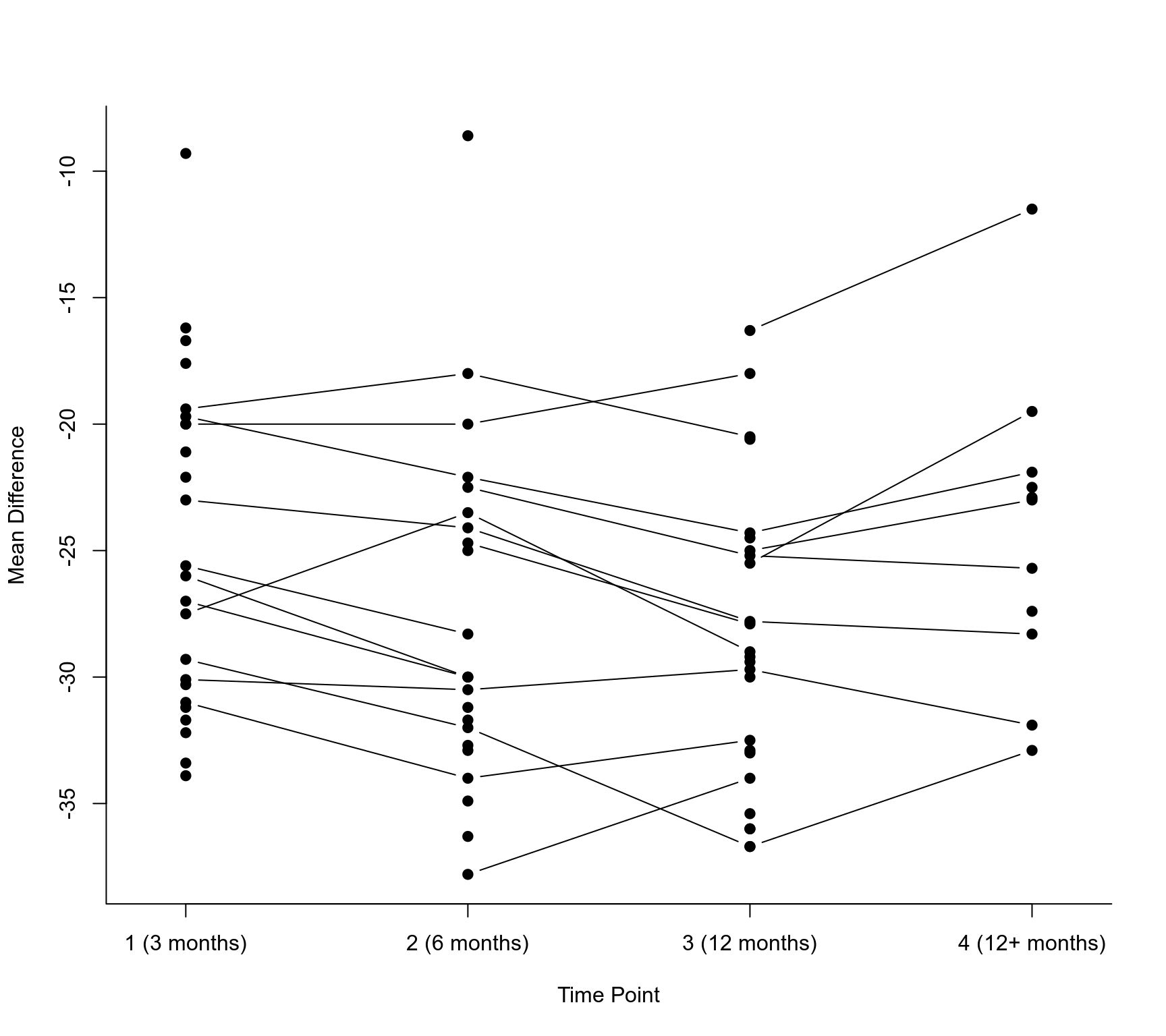
with(dat, interaction.plot(time, study, yi, type="b", pch=19, lty="solid", xaxt="n",
          legend=FALSE, xlab="Time Point", ylab="Mean Difference", bty="l"))
axis(side=1, at=1:4, lab=c("1 (3 months)", "2 (6 months)", "3 (12 months)", "4 (12+ months)"))


### multivariate model with heteroscedastic AR(1) structure for the true effects
res <- rma.mv(yi, V, mods = ~ 0 + factor(time), random = ~ time | study,
              struct = "HAR", data = dat)
print(res, digits=2)
#> 
#> Multivariate Meta-Analysis Model (k = 82; method: REML)
#> 
#> Variance Components:
#> 
#> outer factor: study (nlvls = 46)
#> inner factor: time  (nlvls = 4)
#> 
#>            estim  sqrt  k.lvl  fixed  level 
#> tau^2.1    22.73  4.77     24     no      1 
#> tau^2.2    33.73  5.81     22     no      2 
#> tau^2.3    26.14  5.11     25     no      3 
#> tau^2.4    31.18  5.58     11     no      4 
#> rho         0.88                  no        
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 78) = 856.16, p-val < .01
#> 
#> Test of Moderators (coefficients 1:4):
#> QM(df = 4) = 873.16, p-val < .01
#> 
#> Model Results:
#> 
#>                estimate    se    zval  pval   ci.lb   ci.ub      
#> factor(time)1    -25.90  1.01  -25.60  <.01  -27.89  -23.92  *** 
#> factor(time)2    -27.46  1.14  -24.08  <.01  -29.70  -25.23  *** 
#> factor(time)3    -28.66  1.03  -27.76  <.01  -30.68  -26.63  *** 
#> factor(time)4    -26.49  1.38  -19.17  <.01  -29.20  -23.79  *** 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>