Studies on the Reliability of the CES-D Scale
dat.bonett2010.RdResults from 9 studies on the reliability of the Center for Epidemiologic Studies Depression (CES-D) Scale administered to children providing care to an elderly parent.
dat.bonett2010Format
The data frame contains the following columns:
| study | numeric | study number |
| source | character | source of data |
| ni | numeric | sample size |
| mi | numeric | number of items in the scale |
| ai | numeric | observed value of Cronbach's alpha |
| caregivers | character | gender of the children in the sample |
Details
The Center for Epidemiologic Studies Depression (CES-D) Scale is a 20-item questionnaire assessing various symptoms of depression, with each item scored on a 4-point scale. The scale has been used in several studies to examine depressive symptoms in children providing care to an elderly parent. The dataset includes information on the reliability of the scale as measured with Cronbach's alpha in 9 such studies. Also, the gender composition of the children in each sample is indicated.
Source
Bonett, D. G. (2010). Varying coefficient meta-analytic methods for alpha reliability. Psychological Methods, 15(4), 368–385. https://doi.org/10.1037/a0020142
References
Bonett, D. G. (2002). Sample size requirements for testing and estimating coefficient alpha. Journal of Educational and Behavioral Statistics, 27(4), 335–340. https://doi.org/10.3102/10769986027004335
Hakstian, A. R., & Whalen, T. E. (1976). A k-sample significance test for independent alpha coefficients. Psychometrika, 41(2), 219–231. https://doi.org/10.1007/BF02291840
Concepts
psychology, Cronbach's alpha, reliability generalization, meta-regression
Examples
### copy data into 'dat' and examine data
dat <- dat.bonett2010
dat
#> study source ni ai mi caregivers
#> 1 1 Atienza & Parris Stephens (2000) 103 0.93 20 women
#> 2 2 Hooker et al. (2002) 64 0.91 20 mixed
#> 3 3 Martire et al. (1997) 118 0.94 20 women
#> 4 4 Bass et al. (1996) 401 0.89 20 mixed
#> 5 5 Miller et al. (1995) 215 0.90 20 mixed
#> 6 6 Hooker et al. (1992) 51 0.89 20 mixed
#> 7 7 Hooker et al. (2000) 175 0.86 20 mixed
#> 8 8 Brody et al. (1990) 311 0.91 20 mixed
#> 9 9 Brody et al. (1995) 492 0.90 20 women
### load metafor package
library(metafor)
### meta-analysis using the raw alpha values
res <- rma(measure="ARAW", ai=ai, mi=mi, ni=ni, data=dat)
res
#>
#> Random-Effects Model (k = 9; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.0004 (SE = 0.0003)
#> tau (square root of estimated tau^2 value): 0.0199
#> I^2 (total heterogeneity / total variability): 81.02%
#> H^2 (total variability / sampling variability): 5.27
#>
#> Test for Heterogeneity:
#> Q(df = 8) = 37.9808, p-val < .0001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> 0.9052 0.0077 118.2471 <.0001 0.8902 0.9202 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### meta-analysis using transformed alpha values (using the
### transformation suggested by Hakstian & Whalen, 1976)
res <- rma(measure="AHW", ai=ai, mi=mi, ni=ni, data=dat)
res
#>
#> Random-Effects Model (k = 9; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.0011 (SE = 0.0007)
#> tau (square root of estimated tau^2 value): 0.0328
#> I^2 (total heterogeneity / total variability): 81.43%
#> H^2 (total variability / sampling variability): 5.39
#>
#> Test for Heterogeneity:
#> Q(df = 8) = 35.1131, p-val < .0001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> 0.5440 0.0125 43.4201 <.0001 0.5195 0.5686 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
predict(res, transf=transf.iahw)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 0.9052 0.8891 0.9197 0.8555 0.9420
#>
### meta-analysis using transformed alpha values (using the
### transformation suggested by Bonett, 2002)
res <- rma(measure="ABT", ai=ai, mi=mi, ni=ni, data=dat)
res
#>
#> Random-Effects Model (k = 9; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of total heterogeneity): 0.0461 (SE = 0.0302)
#> tau (square root of estimated tau^2 value): 0.2147
#> I^2 (total heterogeneity / total variability): 81.40%
#> H^2 (total variability / sampling variability): 5.38
#>
#> Test for Heterogeneity:
#> Q(df = 8) = 33.3957, p-val < .0001
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> 2.3561 0.0824 28.6085 <.0001 2.1947 2.5175 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
predict(res, transf=transf.iabt)
#>
#> pred ci.lb ci.ub pi.lb pi.ub
#> 0.9052 0.8886 0.9193 0.8512 0.9396
#>
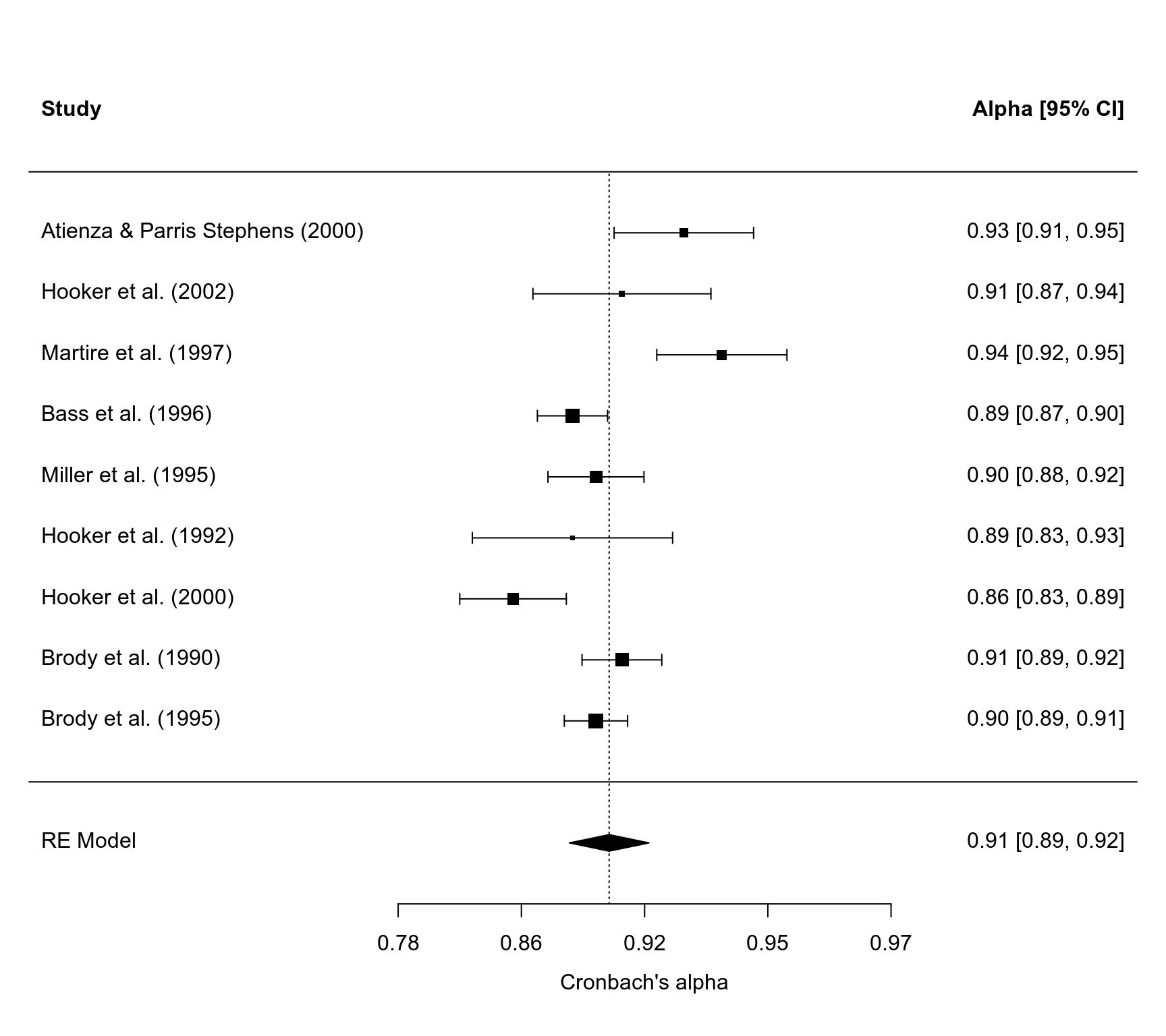
### forest plot
forest(res, slab=source, header=TRUE, top=2, xlim=c(0,4.5),
atransf=transf.iabt, refline=coef(res))
### examine whether female/mixed samples yield different alphas (with raw alphas)
res <- rma(measure="ARAW", ai=ai, mi=mi, ni=ni, mods = ~ caregivers, data=dat)
res
#>
#> Mixed-Effects Model (k = 9; tau^2 estimator: REML)
#>
#> tau^2 (estimated amount of residual heterogeneity): 0.0003 (SE = 0.0002)
#> tau (square root of estimated tau^2 value): 0.0159
#> I^2 (residual heterogeneity / unaccounted variability): 71.80%
#> H^2 (unaccounted variability / sampling variability): 3.55
#> R^2 (amount of heterogeneity accounted for): 36.19%
#>
#> Test for Residual Heterogeneity:
#> QE(df = 7) = 26.6797, p-val = 0.0004
#>
#> Test of Moderators (coefficient 2):
#> QM(df = 1) = 4.3519, p-val = 0.0370
#>
#> Model Results:
#>
#> estimate se zval pval ci.lb ci.ub
#> intrcpt 0.8949 0.0083 107.7806 <.0001 0.8786 0.9111 ***
#> caregiverswomen 0.0277 0.0133 2.0861 0.0370 0.0017 0.0536 *
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
predict(res, newmods=c(0,1), digits=2)
#>
#> pred se ci.lb ci.ub pi.lb pi.ub
#> 1 0.89 0.01 0.88 0.91 0.86 0.93
#> 2 0.92 0.01 0.90 0.94 0.89 0.96
#>