Dataset on Situation Awareness and Task Performance Associations
dat.bakdash2021.RdResults from 77 papers with 678 effects evaluating associations among measures of situation awareness and task performance.
dat.bakdash2021Format
The data frame contains the following columns:
| Author | character | paper author(s) |
| Year | integer | year of paper publication |
| Title | character | title of paper |
| DOI | character | digital object identifier (DOI) |
| DTIC.link | character | permanent link for Defense Technical Information Collection (DITC) reports; see: https://www.dtic.mil |
| SA.measure.type | character | type of SA measure |
| Sample.size | integer | reported sample size |
| Sample.size.stats | integer | reported sample size based on reported statistics (this reflects excluded participants) |
| es.z | numeric | z-transformed correlation coefficient; includes ghost results (disclosed and undisclosed non-significant effects not reported in detail) imputed using the draw method described in Bakdash et al. (2021a) |
| vi.z | numeric | variance for z-transformed correlation (calculated using Sample.size.stats, not Sample.size) |
| SampleID | character | unique identifier for each experiment/study |
| Outcome | integer | unique value for each effect size |
Details
The dataset contains behavioral experiments from 77 papers/79 studies with a total of 678 effects, evaluating associations among measures of situation awareness (“knowing what is going on”) and task performance. Examples of situation awareness include knowledge of current vehicle speed in a simulated driving task and location and heading of aircraft in a simulated air traffic control task. Corresponding examples of task performance include “the number of collisions in a simulated driving task” and “subject matter expert rating of conflict management in a simulated air control task” (Bakdash et al. 2021a, p. 2). This dataset and the ‘Examples’ are a highly simplified version of the data and code in Bakdash et al. (2021b; 2021c). The journal article by Bakdash et al. (2021a) describes the systematic review and meta-analysis in detail.
This dataset is used to illustrate multilevel multivariate meta-analytic models for the overall pooled effect and pooled effects by situation awareness measure. We also adjust meta-analytic models using cluster-robust variance estimation / cluster-robust inference with the robust function in metafor. Results are shown graphically in a customized forest plot with a prediction interval (estimated plausible range of individual effects). Last, we create a table summarizing the estimated meta-analytic heterogeneity parameters.
The meta-analytic results show most pooled effect sizes in the positive medium range or less. There was also substantial meta-analytic heterogeneity (estimated systematic variance in true effects), nearing the magnitude of the overall pooled effect. We interpret the meta-analytic results as situation awareness typically having limited validity for task performance (i.e., good situation awareness does not tend to have strong probabilistic links with good performance and vice-versa). More formally, measures of situation awareness do not generally and meaningfully capture cognitive processes and other relevant factors underlying task performance.
Run-Time
The code run-time can be greatly sped-up using a linear algebra library with R that makes use of multiple CPU cores. See: https://www.metafor-project.org/doku.php/tips:speeding_up_model_fitting. To measure the run-time, uncomment these three lines: start.time <- Sys.time(), end.time <- Sys.time(), and end.time - start.time. Run-times on Windows 10 x64 with the Intel Math Kernel Library are:
| CPU | Run-Time (Minutes) | |
| i7-11850H | 2.49 | |
| i7-4770 | 5.38 |
Source
Bakdash, J. Z., Marusich, L. R., Cox, K. R., Geuss, M. N., Zaroukian, E. G., & Morris, K. M. (2021b). The validity of situation awareness for performance: A meta-analysis (Code Ocean Capsule). https://doi.org/10.24433/CO.1682542.v4
Bakdash, J. Z., Marusich, L. R., Cox, K. R., Geuss, M. N., Zaroukian, E. G., & Morris, K. M. (2021c). The validity of situation awareness for performance: A meta-analysis (Systematic Review, Data, and Code). https://doi.org/10.17605/OSF.IO/4K7ZV
References
Bakdash, J. Z., Marusich, L. R., Cox, K. R., Geuss, M. N., Zaroukian, E. G., & Morris, K. M. (2021a). The validity of situation awareness for performance: A meta-analysis. Theoretical Issues in Ergonomics Science, 1–24. https://doi.org/10.1080/1463922X.2021.1921310
Supplemental materials: https://www.tandfonline.com/doi/suppl/10.1080/1463922X.2021.1921310/suppl_file/ttie_a_1921310_sm5524.docx
Concepts
psychology, human factors, engineering, correlation coefficients, multilevel models, multivariate models, cluster-robust inference
Examples
### copy data into 'dat' and examine data
dat <- dat.bakdash2021
head(dat[c(1,2,6,8:12)])
#> Author Year SA.measure.type Sample.size.stats es.z vi.z
#> 1 Cummings and Guerlain 2007 SPAM 42 0.4623530 0.02564103
#> 2 Cummings and Guerlain 2007 SAGAT 42 0.1498943 0.02564103
#> 3 Durso 1998 SPAM 12 0.3775238 0.11111111
#> 4 Durso 1998 SAGAT 12 0.3932583 0.11111111
#> 5 Durso 2006 SPAM 77 0.1423756 0.01351351
#> 6 Durso 2006 SPAM 80 0.3058401 0.01298701
#> SampleID Outcome
#> 1 Cummings and Guerlain2007 1
#> 2 Cummings and Guerlain2007 2
#> 3 Durso1998 3
#> 4 Durso1998 4
#> 5 Durso 2006 5
#> 6 Durso 2006 6
#start.time <- Sys.time()
### load metafor
library(metafor)
### multilevel meta-analytic model to get the overall pooled effect
res.overall <- rma.mv(es.z, vi.z, mods = ~ 1,
random = ~ 1 | SampleID / Outcome,
data = dat,
test = "t")
res.overall
#>
#> Multivariate Meta-Analysis Model (k = 678; method: REML)
#>
#> Variance Components:
#>
#> estim sqrt nlvls fixed factor
#> sigma^2.1 0.0298 0.1725 79 no SampleID
#> sigma^2.2 0.0147 0.1212 678 no SampleID/Outcome
#>
#> Test for Heterogeneity:
#> Q(df = 677) = 1441.6490, p-val < .0001
#>
#> Model Results:
#>
#> estimate se tval df pval ci.lb ci.ub
#> 0.2692 0.0240 11.2329 677 <.0001 0.2222 0.3163 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### get prediction interval
predict(res.overall)
#>
#> pred se ci.lb ci.ub pi.lb pi.ub
#> 0.2692 0.0240 0.2222 0.3163 -0.1474 0.6858
#>
### cluster-robust variance estimation (CRVE) / cluster-robust inference
res.overall.crve <- robust(res.overall, cluster = SampleID)
res.overall.crve
#>
#> Multivariate Meta-Analysis Model (k = 678; method: REML)
#>
#> Variance Components:
#>
#> estim sqrt nlvls fixed factor
#> sigma^2.1 0.0298 0.1725 79 no SampleID
#> sigma^2.2 0.0147 0.1212 678 no SampleID/Outcome
#>
#> Test for Heterogeneity:
#> Q(df = 677) = 1441.6490, p-val < .0001
#>
#> Number of estimates: 678
#> Number of clusters: 79
#> Estimates per cluster: 1-64 (mean: 8.58, median: 4)
#>
#> Model Results:
#>
#> estimate se¹ tval¹ df¹ pval¹ ci.lb¹ ci.ub¹
#> 0.2692 0.0239 11.2408 78 <.0001 0.2215 0.3169 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> 1) results based on cluster-robust inference (var-cov estimator: CR1,
#> approx t-test and confidence interval, df: residual method)
#>
### get prediction interval
res.overall.crve.pred <- predict(res.overall.crve)
res.overall.crve.pred
#>
#> pred se ci.lb ci.ub pi.lb pi.ub
#> 0.2692 0.0239 0.2215 0.3169 -0.1532 0.6916
#>
### multilevel meta-analytic model for SA measures
res.sa <- rma.mv(es.z, vi.z, mods = ~ SA.measure.type - 1,
random = ~ 1 | SampleID / Outcome,
data = dat,
test = "t")
res.sa
#>
#> Multivariate Meta-Analysis Model (k = 678; method: REML)
#>
#> Variance Components:
#>
#> estim sqrt nlvls fixed factor
#> sigma^2.1 0.0314 0.1773 79 no SampleID
#> sigma^2.2 0.0122 0.1104 678 no SampleID/Outcome
#>
#> Test for Residual Heterogeneity:
#> QE(df = 668) = 1238.1070, p-val < .0001
#>
#> Test of Moderators (coefficients 1:10):
#> F(df1 = 10, df2 = 668) = 15.7060, p-val < .0001
#>
#> Model Results:
#>
#> estimate se tval df pval ci.lb ci.ub
#> SA.measure.typeDirect-SR 0.3781 0.1131 3.3437 668 0.0009 0.1561 0.6002 ***
#> SA.measure.typeExplicit Recall 0.2297 0.0732 3.1366 668 0.0018 0.0859 0.3734 **
#> SA.measure.typeGeneral Know. 0.2161 0.0570 3.7941 668 0.0002 0.1043 0.3279 ***
#> SA.measure.typeMARS 0.1904 0.0980 1.9428 668 0.0525 -0.0020 0.3828 .
#> SA.measure.typeOther 0.4345 0.0584 7.4358 668 <.0001 0.3197 0.5492 ***
#> SA.measure.typeSABARS 0.3045 0.0996 3.0570 668 0.0023 0.1089 0.5000 **
#> SA.measure.typeSAGAT 0.2954 0.0330 8.9551 668 <.0001 0.2306 0.3602 ***
#> SA.measure.typeSARS 0.3347 0.1074 3.1172 668 0.0019 0.1239 0.5455 **
#> SA.measure.typeSART 0.1582 0.0392 4.0324 668 <.0001 0.0812 0.2353 ***
#> SA.measure.typeSPAM 0.2884 0.0399 7.2259 668 <.0001 0.2100 0.3667 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
### cluster-robust variance estimation (CRVE) / cluster-robust inference
res.sa.crve <- robust(res.sa, cluster = SampleID)
res.sa.crve
#>
#> Multivariate Meta-Analysis Model (k = 678; method: REML)
#>
#> Variance Components:
#>
#> estim sqrt nlvls fixed factor
#> sigma^2.1 0.0314 0.1773 79 no SampleID
#> sigma^2.2 0.0122 0.1104 678 no SampleID/Outcome
#>
#> Test for Residual Heterogeneity:
#> QE(df = 668) = 1238.1070, p-val < .0001
#>
#> Number of estimates: 678
#> Number of clusters: 79
#> Estimates per cluster: 1-64 (mean: 8.58, median: 4)
#>
#> Test of Moderators (coefficients 1:10):¹
#> F(df1 = 10, df2 = 69) = 99.4115, p-val < .0001
#>
#> Model Results:
#>
#> estimate se¹ tval¹ df¹ pval¹ ci.lb¹ ci.ub¹
#> SA.measure.typeDirect-SR 0.3781 0.0552 6.8448 69 <.0001 0.2679 0.4884 ***
#> SA.measure.typeExplicit Recall 0.2297 0.0608 3.7776 69 0.0003 0.1084 0.3510 ***
#> SA.measure.typeGeneral Know. 0.2161 0.0447 4.8381 69 <.0001 0.1270 0.3052 ***
#> SA.measure.typeMARS 0.1904 0.1629 1.1686 69 0.2466 -0.1346 0.5154
#> SA.measure.typeOther 0.4345 0.0861 5.0486 69 <.0001 0.2628 0.6061 ***
#> SA.measure.typeSABARS 0.3045 0.0759 4.0110 69 0.0002 0.1530 0.4559 ***
#> SA.measure.typeSAGAT 0.2954 0.0375 7.8809 69 <.0001 0.2206 0.3702 ***
#> SA.measure.typeSARS 0.3347 0.0694 4.8208 69 <.0001 0.1962 0.4731 ***
#> SA.measure.typeSART 0.1582 0.0361 4.3805 69 <.0001 0.0862 0.2303 ***
#> SA.measure.typeSPAM 0.2884 0.0383 7.5331 69 <.0001 0.2120 0.3647 ***
#>
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> 1) results based on cluster-robust inference (var-cov estimator: CR1,
#> approx t/F-tests and confidence intervals, df: residual method)
#>
### profile likelihood plots
par(mfrow=c(2,1))
profile(res.sa.crve, progbar = FALSE)
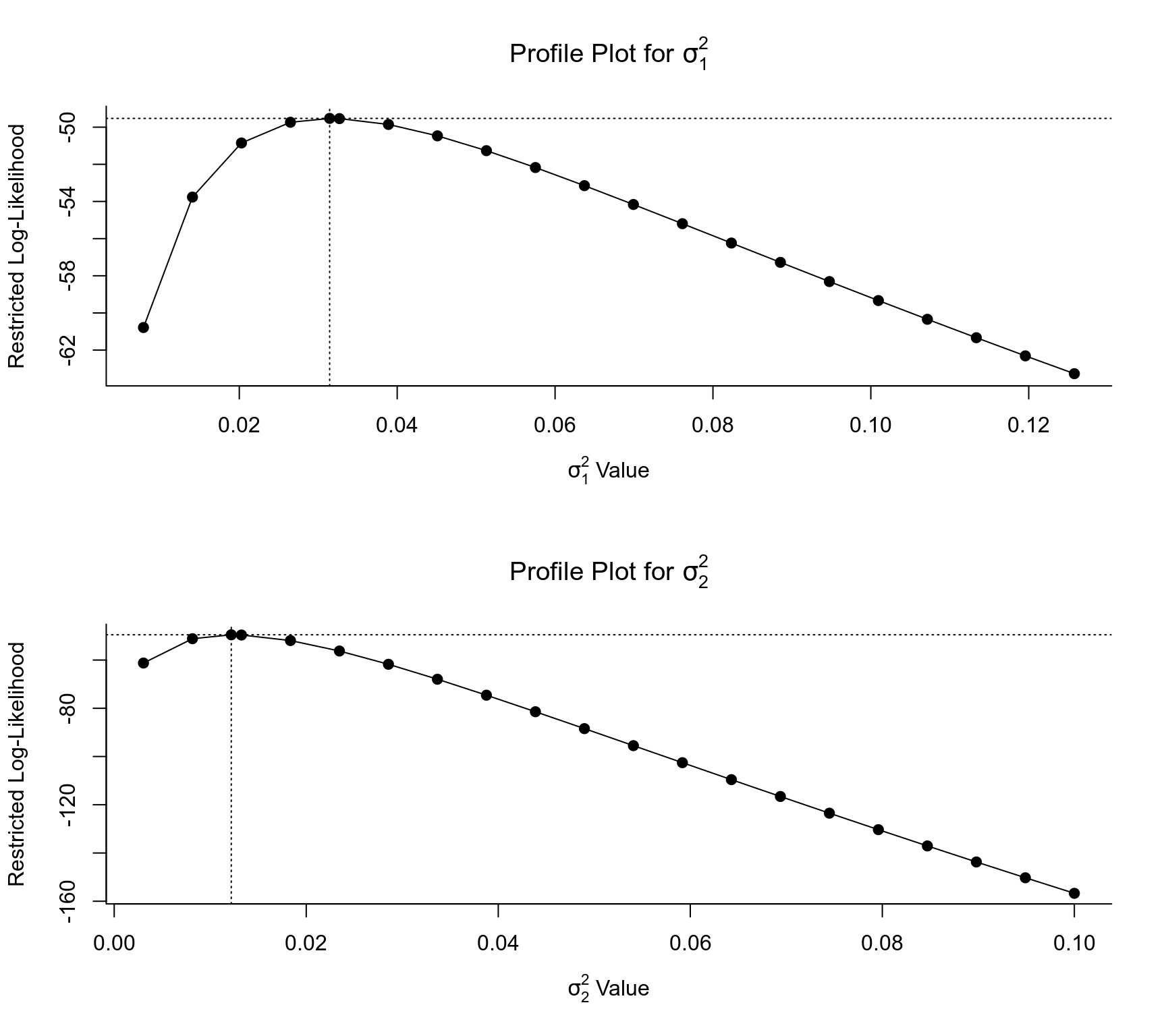### format and combine output of meta-analytic models for the forest plot
all.z <- c(res.sa.crve$beta, # SA measures
res.overall.crve$beta, # pooled effect for confidence interval (CI)
res.overall.crve$beta) # pooled effect for prediction interval (PI)
all.ci.lower <- c(res.sa.crve$ci.lb, # SA measures
res.overall.crve.pred$ci.lb, # pooled effect, lower CI
res.overall.crve.pred$pi.lb) # pooled effect, lower PI
all.ci.upper <- c(res.sa.crve$ci.ub, # SA measures
res.overall.crve.pred$ci.ub, # pooled effect, upper CI
res.overall.crve.pred$pi.ub) # pooled effect, upper PI
### note: there is no p-value for the PI
all.pvals <- c(res.sa.crve$pval, res.overall.crve$pval)
all.labels <- c(sort(unique(dat$SA.measure.type)), "Overall", "95% Prediction Interval")
### function to round p-values for the forest plot
pvals.round <- function(input) {
input <- ifelse(input < 0.001, "< 0.001",
ifelse(input < 0.01, "< 0.01",
ifelse(input < 0.05 & input >= 0.045, "< 0.05",
ifelse(round(input, 2) == 1.00, "0.99",
sprintf("%.2f", round(input, 2))))))}
all.pvals.rounded <- pvals.round(all.pvals)
### forest plot
plot.vals <- data.frame(all.labels, all.z, all.ci.lower, all.ci.upper)
par(mfrow=c(1,1), cex = 1.05)
forest(plot.vals$all.z,
ci.lb = plot.vals$all.ci.lower,
ci.ub = plot.vals$all.ci.upper,
slab = plot.vals$all.labels,
psize = 1,
efac = 0, xlim = c(-1.8, 2.5), clim = c(-1, 1),
transf = transf.ztor, # transform z to r
at = seq(-0.5, 1, by = 0.25),
xlab = expression("Correlation Coefficient"~"("*italic('r')*")"),
main = "\n\n\nSA Measures",
ilab = c(all.pvals.rounded, ""), ilab.xpos = 2.45, ilab.pos = 2.5,
digits = 2, refline = 0, annotate = FALSE)
### keep trailing zero using sprintf
output <- cbind(sprintf("%.2f", round(transf.ztor(plot.vals$all.z), 2)),
sprintf("%.2f", round(transf.ztor(plot.vals$all.ci.lower), 2)),
sprintf("%.2f", round(transf.ztor(plot.vals$all.ci.upper), 2)))
### alignment kludge
annotext <- apply(output, 1, function(x) {paste0(" ", x[1], " [", x[2],", ", x[3], "]")})
text( 1.05, 12:1, annotext, pos = 4, cex = 1.05)
text(-1.475, 14.00, "SA Measure", cex = 1.05)
text( 2.30, 14.00, substitute(paste(italic('p-value'))), cex = 1.05)
text( 1.55, 14.00, "Correlation [95% CI]", cex = 1.05)
abline(h = 1.5)
### black polygon for overall mean CIs
addpoly(all.z[11], ci.lb = all.ci.lower[11], ci.ub = all.ci.upper[11],
rows = 2, annotate = FALSE, efac = 1.5, transf = transf.ztor)
### white polygon for PI
addpoly(all.z[12], ci.lb = all.ci.lower[12], ci.ub = all.ci.upper[12],
rows = 1, col = "white", border = "black",
annotate = FALSE, efac = 1.5, transf = transf.ztor)
par(mfrow=c(1,1), cex = 1) # reset graph parameters to default
### confidence intervals for the variance components
re.CI.variances <- confint(res.overall)
re.CI.variances
#>
#> estimate ci.lb ci.ub
#> sigma^2.1 0.0298 0.0179 0.0490
#> sigma.1 0.1725 0.1338 0.2213
#>
#> estimate ci.lb ci.ub
#> sigma^2.2 0.0147 0.0101 0.0204
#> sigma.2 0.1212 0.1003 0.1429
#>
sigma1.z <- data.frame(re.CI.variances[[1]]["random"])
sigma2.z <- data.frame(re.CI.variances[[2]]["random"])
### fit model using alternative multivariate parameterization
res.overall.alt <- rma.mv(es.z, vi.z, mods = ~ 1,
random = ~ factor(Outcome) | factor(SampleID),
data = dat,
test = "t")
### confidence intervals for the total amount of heterogeneity variance component
res.overall.alt.tau <- confint(res.overall.alt, tau2=1)$random
### I^2: http://www.metafor-project.org/doku.php/tips:i2_multilevel_multivariate
W <- diag(1/dat$vi.z)
X <- model.matrix(res.overall)
P <- W - W %*% X %*% solve(t(X) %*% W %*% X) %*% t(X) %*% W
### I^2 (variance due to heterogeneity): 61%
I2 <- 100 * res.overall.alt$tau2 /
(res.overall.alt$tau2 + (res.overall$k-res.overall$p)/sum(diag(P)))
I2
#> [1] 60.99124
### 95% CI for I^2 using uncertainty around tau^2
I2.CI.lb <- 100 * res.overall.alt.tau[1,2] /
(res.overall.alt.tau[1,2] + (res.overall$k-res.overall$p)/sum(diag(P)))
I2.CI.lb
#> [1] 53.00297
I2.CI.ub <- 100 * res.overall.alt.tau[1,3] /
(res.overall.alt.tau[1,3] + (res.overall$k-res.overall$p)/sum(diag(P)))
I2.CI.ub
#> [1] 69.15562
### total amount of heterogeneity (tau)
sqrt(res.overall.alt$tau2)
#> [1] 0.2108226
### heterogeneity table
table.heterogeneity <- data.frame(matrix(ncol = 3, nrow = 4))
colnames(table.heterogeneity) <- c("Parameter Value",
"Lower 95% CI",
"Upper 95% CI")
rownames(table.heterogeneity) <- c("Tau (Total)",
"Tau1 (Between paper)",
"Tau2 (Within paper)",
"I2 (%)")
table.heterogeneity[1,] <- res.overall.alt.tau[2,]
table.heterogeneity[2,] <- sigma1.z[2,]
table.heterogeneity[3,] <- sigma2.z[2,]
table.heterogeneity[4,] <- c(I2, I2.CI.lb, I2.CI.ub)
round(table.heterogeneity, 2)
#> Parameter Value Lower 95% CI Upper 95% CI
#> Tau (Total) 0.21 0.18 0.25
#> Tau1 (Between paper) 0.17 0.13 0.22
#> Tau2 (Within paper) 0.12 0.10 0.14
#> I2 (%) 60.99 53.00 69.16
#end.time <- Sys.time()
#end.time - start.time